1. у=4х-2
1)
х=0 у=4*0-2=-2
х=6 у=4*6-2=10
2)
у=0
4х-2=0
4х=2
х=0,5
у=2
4х-2=2
4х=4
х=1
2.
Пересечение с осью ОХ:
у=0
1,2х-24=0
1,2х=24
х=20
(20; 0)
Пересечение с осью ОУ:
х=0
у=1,2*0-24
у=-24
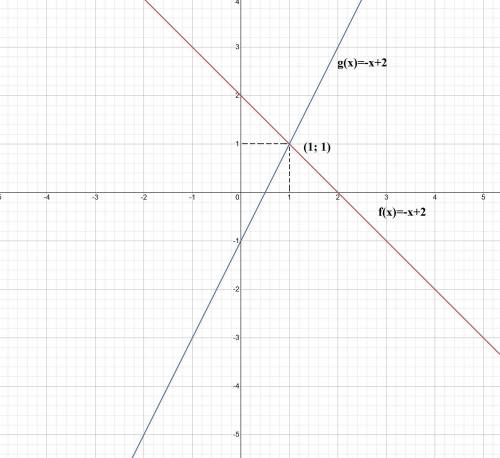
3. Поскольку оба графика линейные функции, то для построения достаточно 2х точек:
f(x)=-x+2
x y
0 2
1 1
g(x)=2x-1
x y
0 -1
2 3
1) Из графика видно, что точка пересечения (1; 1)
2) Из построенных графиков видно, что g(x)>f(x), при х>1.
4. График линейной функции имеет вид:
у=kx+b
a График проходит через точки (0; 0), (1; 1)
0=k*0+b ⇒b=0
1=k*1 ⇒k=1
у=х
б) Графиком является постоянная функция:
у=-2
в) График проходит через точки (0; 3) и (3;0)
3=0*k+b ⇒b=3
0=3k+b
3k=0-3
k=-1
y=-x+3
Геометрический смысл производной: значение производной в точке касания является угловым коэффициентом касательной. Т.к. f'(-3)=-1.25=k
уравнение касательной: y=kx+b=-1.25x+b.
Имея точку касания B(-3;3) найдем коэффициент b:
-1.25*(-3)+b=3
3.75+b=3
b=-0.75
y=-1.25x-0.75
Тогда:
-1.25х-0.75=0
-1.25х=0.75
х=-0.6
Абсцисса точки пересечения касательной с осью OX х=-0.6.