Объяснение:
Чтобы узнать какой цифрой оканчивается число:
Делим показатель степени на число вариантов, тоесть на количество цифр, которыми может оканчиваться число в разных целых положительных степенях, далее смотрим по остатку, который останется (или не останется. если нацело) при делении.
Рассмотрим отдельно каждое слагаемое данной суммы.
54¹=54, оканчивается на 4 (первый вариант, если при делении, указанном выше, остаток получится 1)
54²= 2916, оканчивается на 6 (второй вариант, если при делении остаток получится 2 (нацело))
Вариантов 2.
35÷2= 17 (остаток 1), тогда нам подходит первый вариант, тоесть 54³⁵ будет оканчиваться на 4.
Рассмотрим 28²¹
28¹=28, оканчивается на 8 (первый вариант, если получится остаток 1)
28²=784, оканчивается на 4 (второй вариант, если выйдет остаток 2)
28³=21952, оканчивается на 2 (третий вариант, если получится остаток 3)
28⁴=614656, оканчивается на 6 (четвертый вариант, если получится остаток 4 (нацело))
Вариантов 4.
21÷4=5 (остаток 1), значит первый вариант, тоесть 28²¹ будет оканчиваться на 8.
Сложим последние цифры чисел в степенях.
4+8=12, оканчивается на 2.
Значит 54³⁵ + 28²¹ оканчивается на 2
ответ: 2
1) 8+2√13 и ли 8-2√13
2 178+35√13 или 178-35√13
(Составим систему и найдём а из первого ур-я, а b² -из второго уравнения)
1) а+b²= (5-b)+(5b-3)=4b-2.
Найдём b
-b²+5b-3=0;
D²=5²-4*(-1)*(-3)=25-12=13
b₁=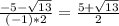
b₂=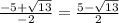
1)Теперь подставим b1 и b2
а)4b-2=4*(5+√13)/2-2= 2*(5+√13)-2=10+2√13-2=8+2√13
б)4b-2=4*(5-√13)/2-2= 2*(5-√13)-2=10-2√13-2=8-2√13
2)a³b²+a²b³=ab*a(a*b +b²)=3*( 5-b)(3+(5b-3))=15b*(5-b)=75b-b²=75b-(5b-3)=
=75b-5b+3=70b+3.
Теперь подставим b1 и b2
а) 70(5+√13)/2+3=35*5+35√13+3=178+35√13
,)70(5-√13)/2+3=35*5-35√13+3=178-35√13