Объяснение:
2^(2x+1) + 25^(0,5+x) >= 7*10^x
1) (2^2x)*(2^1) + (25^0,5)*(25^x) - 7*10^x >= 0;
2) 2*2^2x + 5*5^2x - 7*2^x*5^x >= 0;
3) Заменим 2^x на t и 5^x на m, тогда 2*t^2 + 5*m^2 - 7*t*m >= 0;
4) Разделим каждый член неравенства на 5*m^2;
5) 2t^2/5m^2 - 7t/5m + 1 >= 0;
6) Разложить на множители
(t/m - 1)*(t/m - 5/2) >= 0;
7) На числовой прямой отмечаем точки 1 и 5/2, определяет знаки на промежутках. Получаем t/m принадлежит (-∞;1]и[5/2;+∞)
8) Обратная замена: (2/5)^x
9) (2/5)^x принадлежит
(-∞;1]и[5/2;+∞), следовательно
x принадлежит (-∞;0]и[-1;+∞)
1. x^2-4x+40≤0
D = b^2−4ac = 16-160 = -144
D < 0 ⇒ нет корней
Т.к. a = 1 > 0, то x^2−4x+40 > 0 для любых x, следовательно, неравенство x^2-4x+40 ≤ 0 не имеет смысла.
ответ: x∈∅, решений нет.
2. x^2-4x+40<0
Аналогично, как для п 1.
Т.к. a = 1 > 0, то x^2−4x+40 > 0 для любых x, следовательно, неравенство x^2-4x+40 < 0 не имеет смысла.
ответ: x∈∅, решений нет.
3. x^2-4x+4>0
D = 16-16 = 0
D = 16-16 = 0 ⇒ 1 корень
x = -b/2 = 4/2 = 2
Вычислим знаки на каждом интервале:
x<2 | x>2
+ | +
Неравенство строгое, значит точка с абсциссой x=2 — выколотая.
ответ: x∈(−∞; 2)∪(2; +∞) или x<2; x>2.
4. x^2-4x+4≥0
x = 2 (см п. 3.)
Вычислим знаки на каждом интервале:
x<2 | x>2
+ | +
Неравенство нестрогое, значит точка с абсциссой x=2 — входит в решение.
ответ: x∈(−∞; +∞) или x — любое число, x∈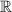 .
.
Пусть х (км/ч) - скорость пешехода из пункта А, тогда скорость пешехода из пункта В - (9-х) (км/ч).
20/х (ч) - половина расстояния пешеход из пункта А, а пешеход из В - за 20 / (9-х) ч. На 20/х-20 / (9-х) - пешеход проходит из пункта В полпути быстрее (1 час).
* 40-4=36 (км за 4 часа пешеходы.
* 36:4=9 (км/ч) - скорость сближения.
Составим уравнение:
20/x (дробью) - 20 / (9-x) (дробью) = 1 |*х (9-х)
180-20 х-20 х=9 х-х ²
х ²-9 х-40 х+180=0
х²-49 х+180=0
D=2401-720=1681
х1,2=49 ±41/2
х1=4 (км/ч)
х2=45 (для пешехода невозможна т. к 9-45<0).
9-4=5 (км/ч)
ответ: пешеход, который проходил из пункта А в пункт В, шёл со скоростью 4 км/ч, а пешеход, который проходил из В в А, шёл со скоростью 5 км/ч.