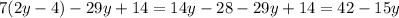
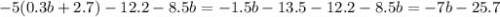
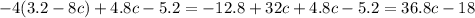
Объяснение:
Для того, чтобы упростить выражение (b - 3)(b - 4) - (b + 4)2 мы откроем скобки, а затем выполним группировку и приведение подобных слагаемых.
Открывать скобки будем с правила умножения скобки на скобку, формулу сокращенного умножения квадрат суммы и правило открытия скобок перед которыми стоит минус.
Откроем скобки и получим выражение:
(b - 3)(b - 4) - (b + 4)2 = b2 - 4b - 3b + 12 - b2 - 8b - 16.
Выполним приведение подобных слагаемых.
b2 - 4b - 3b + 12 - b2 - 8b - 16 = b2 - b2 - 8b - 4b - 3b + 12 - 16 = -15b - 4.
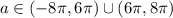
Объяснение:
Все ненулевые решения разбиваются на пары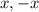 
. Чтобы у уравнения было 8 корней, у него должно быть ровно 4 положительных корня, и 0 не должен являться корнем. Дальше будем думать только о неотрицательных корнях.
Уравнение с косинусом легко решается:
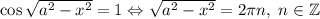
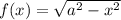— функция, которая убывает от 
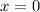до 
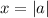, принимая все значения от 
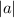до 0.
Значит, чтобы условие было выполнено, в промежуток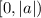 
должны попасть ровно 4 числа вида 
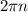. Понятно, что в промежуток попадут 0, 2π, 4π, 6π — и не попадут 8π и т.д.
Условие этого:
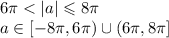
При этом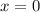 
не должен быть решением, поэтому 
, 
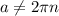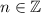. Это удалит из решения 
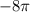и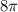 
.
