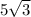 ;
; 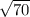 ;
; 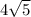
16 (км/час) - скорость яхты в неподвижной воде
Объяснение:
х - скорость яхты в неподвижной воде
х+2 - скорость яхты по течению
х-2 - скорость яхты против течения
126/(х+2) - время яхты по течению
126/(х-2) - время яхты против течения
34/2=17 - время плота
Согласно условию задачи, яхта вышла позже на 1 час, уравнение:
126/(х+2)+126/(х-2)+1=17
126/(х+2)+126/(х-2)=16 избавляемся от дробного выражения, общий знаменатель (х+2)(х-2), или х²-4. Надписываем над числителями дополнительные множители:
126(х-2)+126(х+2)=16(х²-4)
126х-252+126х+252=16х²-64
-16х²+252х+64=0
16х²-252х-64=0/4
4х²-63х-16=0, квадратное уравнение, ищем корни:
х₁,₂=(63±√3969+256)/8
х₁,₂=(63±√4225)/8
х₁,₂=(63±65)/8
х₁= -2/8 отбрасываем, как отрицательный
х₂=128/8=16 (км/час) - скорость яхты в неподвижной воде
Проверка:
126 : 18 + 126 : 14 +1 =7+9+1=17 (часов) время яхты в пути и на стоянке.
34 : 2 = 17 (часов) - время плота, всё верно.
Для определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов - ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой "30 градусов", на их пересечении считываем результат - одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2 ) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других "популярных" углов.
Объяснение:
Arcsin(ctg(π/4))=arcsin(1)=π/ 2 cos(arcsin(-1/2)-arcsin(1))=cos(2π/3-π/2)= cos(4π/6-3π/6)=cos(π/6)=√3/2.