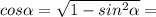Найдите tg(a), если sin(a) = 2 корень из 29\29 [0; пи\2]

👇

Ответ:

эрика95

12.09.2020

Т.к. отрезок [0;pi/2], то cos положительный, т.е. тангенс больше нуля

По основному тригонометрическому тождеству, $cos\alpha=\sqrt{1-sin^2\alpha}=$ $\sqrt{1-(2*\sqrt29/29)^2}=\sqrt{1-4/29}=\sqrt{25/29}=5\sqrt{29}/29$

$tg\alpha=sin\alpha/cos\alpha=$ $(2\sqrt{29}/29)/(5\sqrt{29}/29)=2/5=0,4$

4,8(71 оценок)

Открыть все ответы

Ответ:

Валерияжеле

12.09.2020

Пусть C — первая деталь окажется стандартной. Гипотезы:

H₁ - деталь изготовлена первым заводом;

H₂ - деталь изготовлена вторым заводом;

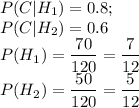
$P(C|H_1)=0.8;\\ P(C|H_2)=0.6\\ P(H_1)=\dfrac{70}{120}=\dfrac{7}{12}\\ P(H_2)=\dfrac{50}{120}=\dfrac{5}{12}$

Вероятность события А по формуле полной вероятности

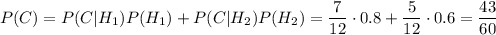
$P(C)=P(C|H_1)P(H_1)+P(C|H_2)P(H_2)=\dfrac{7}{12}\cdot0.8+\dfrac{5}{12}\cdot 0.6=\dfrac{43}{60}$

По формуле Байеса, вероятность того, что эта деталь изготовлена первым заводом, равна:

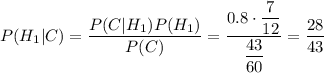
$P(H_1|C)=\dfrac{P(C|H_1)P(H_1)}{P(C)}=\dfrac{0.8\cdot\dfrac{7}{12}}{\dfrac{43}{60}}=\dfrac{28}{43}$

Аналогично, пусть В — вторая деталь окажется стандартной. Так как одна деталь уже вынута, то в партии остается 119 лампочек, из них 69 изготовлены на первом заводе.

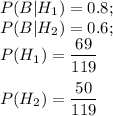
$P(B|H_1)=0.8;\\ P(B|H_2)=0.6;\\ P(H_1)=\dfrac{69}{119}\\ \\ P(H_2)=\dfrac{50}{119}$

По формуле полной вероятности, вероятность события В:

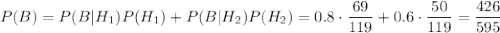
$P(B)=P(B|H_1)P(H_1)+P(B|H_2)P(H_2)=0.8\cdot\dfrac{69}{119}+0.6\cdot\dfrac{50}{119}=\dfrac{426}{595}$

По формуле Байеса, вероятность того, что эта деталь изготовлена первым заводом, равна:

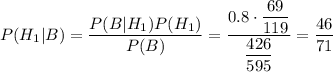
$P(H_1|B)=\dfrac{P(B|H_1)P(H_1)}{P(B)}=\dfrac{0.8\cdot\dfrac{69}{119}}{\dfrac{426}{595}}=\dfrac{46}{71}$

По теореме умножения, вероятность того, что наудачу взятые две лампочки являются стандартными, равна

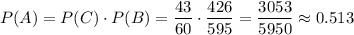
$P(A)=P(C)\cdot P(B)=\dfrac{43}{60}\cdot\dfrac{426}{595}=\dfrac{3053}{5950}\approx0.513$

По теореме умножения, вероятность того, что обе лампочки изготовлены на первом заводе, при условии что событие А произошло, равна:

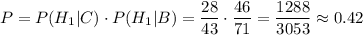
$P=P(H_1|C)\cdot P(H_1|B)=\dfrac{28}{43}\cdot\dfrac{46}{71}=\dfrac{1288}{3053}\approx0.42$

4,5(5 оценок)

Ответ:

Ученик132312

12.09.2020

На первый взгляд задача очень простая.
Зачастую решение таких задач сводят к нахождению объемов параллелепипедов и затем объём большего делят на объём меньшего ( как, кстати, и задач на количество плиток одной площади по поверхности большей площади).
Переводим размеры в одинаковые единицы измерения
Для кузова машины 32дм, 32 дм и 80 дм
для коробок 4 дм, 8 дм и 10 дм
V1:V2=(32•32•80):(4•8•10)=8•4•8=256 (коробок)

НО! Следует заметить, что объёмы могут делиться нацело, а полученное от деления количество коробок не поместится в кузове, т.к. их размеры могут не быть кратными.
На рисунке приложения показан оптимальный вариант размещения коробок.
По условию этой задачи коробки можно разместить в кузове без зазоров, они полностью займут его пространство, т.к. размеры коробки помещается по длине кузова 80:10=8 раз, по ширине 32:8=4 раза и по высоте 32:4=8 раз. Всего поместится 8•8•4=256 коробок.
Если размещать их длиной по высоте кузова, получим три слоя коробок–32:10=3 (два дм высоты останутся незаполненными). Тогда поместится 20•4•3=240 коробок.
Всегда следует высчитывать, сколько раз умещаются размеры меньшей фигуры в размерах большей.

4,6(17 оценок)

Это интересно:

Питомцы-и-животные

07.12.2022

Как приучить кошку ходить в туалет на унитаз...

Транспорт

21.04.2022

Как стать настоящим мастером вождения в стиле Дзен...

Компьютеры-и-электроника

15.02.2023

Как отключить Безопасный поиск в Google на Android: Простой подход для получения наилучшего опыта поиска...

Стиль-и-уход-за-собой