1) Число корней квадратного уравнения можно определить при дискриминанта. Если D=0, то уравнение имеет один корень, если D>0, то уравнение имеет два корня, если D<0, то уравнение действительных корней не имеет.
а) 9х²+12х+4=0
D = 12²-4*9*4 = 144-144 = 0 = 0 ⇒ уравнение имеет один корень.
б) 2х²+3х-11=0
D = 3²-4*4*(-11) = 9+176 = 185 > 0 ⇒ уравнение имеет два корня.
2) а) х²-14+33=0
Уравнение приведенное, проще всего использовать теорему Виета.
х₁*х₂=33
х₁+х₂=14
Отсюда х₁=11, х₂=3
ответ: х₁=11, х₂=3
б) -3х²+10х-3=0
D = 10²-4*(-3)*(-3) = 100-36 = 64
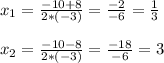
ответ: х₁=1/3, х₂=3
в) х⁴-10х²+9=0
Биквадратное уравнение решим при замены.
х²=t
t²-10t+9=0
По теореме Виета:
t₁*t₂=9
t₁+t₂=10
t₁=9, t₂=1
Производим обратную замену.
х²=9 ⇒ х = ±√9 ⇒ х=±3
х²=1 ⇒ х = ±√1 ⇒ х=±1
ответ: х₁,₂ = ±3, х₃,₄ = ±1.
г) х²+10+22=0
D = 10²-4*1*22 = 100-88 = 12
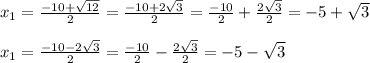
ответ: х₁=-5+√3, х₂=-5-√3
д) х²-110х+216=0
По теореме Виета:
х₁*х₂=216
х₁+х₂=110
х₁ = 108, х₂ = 2
ответ: х₁ = 108, х₂ = 2
3) Пусть одна сторона прямоугольника равна х см. Вторая сторона на 9 см больше первой, поэтому она равна (х+9) см. Площадь прямоугольника 112 см² (по условию). Она находится как произведение смежных сторон прямоугольника.
Составляем уравнение.
х*(х+9) = 112
х²+9х-112 = 0
D = 9²+4*1*112 = 81+448 = 529
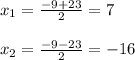
Длина отрицательной быть не может, поэтому нам подходит только один корень: 7
Длина одной стороны прямоугольника 7 см.
Длина второй стороны прямоугольника х+9=7+9=16 см.
ответ: 7 см, 16 см.
4)
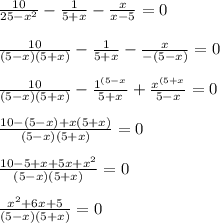
ОДЗ: (5-х)(5+х)≠0 ⇒ х≠5, х≠-5.
х²+6х+5=0
По теореме Виета:
х₁*х₂=5
х₁+х₂=-6
х₁ = 5, х₂ = 1
х₁ = 5 - не удовлетворяет ОДЗ.
ответ: х=1
5) 4х²+рх+9=0
Квадратное уравнение имеет один корень, если дискриминант равен нулю. Найдем дискриминант и приравняем его к нулю. Затем решим получившееся уравнение и тем самым найдем значения р.
D = р²-4*4*9 = р²-144
р²-144 = 0
р²=144
р = ±√144
р= ±12
ответ: р= ±12

Смотри, как решать такие задачи. У тебя вся работа равна 1, если не сказаны конкретные единицы работы. Эта задача крутится по одной формуле: общая работа / скорость ее выполнения = время. Работа в этой формуле известна, время - в условии, неизвестна скорость => берем за переменные неизвестные. Пусть X - скорость выполнения работы первого, а Y - скорость второго, тогда можно составить систему уравнений для задачи:
Почему именно так. Вся работа у нас равна 1, а половина работы - 0,5. Вначале она вместе "делали" работу => скорости складываются, а потом поотдельности и половину работы.
Решая, получаю x= 1/10 и y = 1/15.
Дальше дашь ответ сам, я нашел только скорости, осталось немного.
Надеюсь