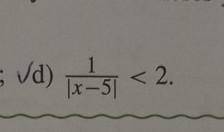
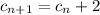означает, что каждый следующий член последовательности будет получаться из предыдущего прибавлением к нему двух.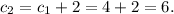
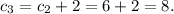
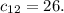
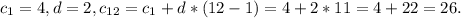
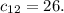
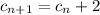означает, что каждый следующий член последовательности будет получаться из предыдущего прибавлением к нему двух.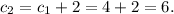
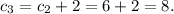
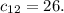
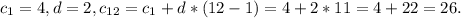
Объяснение:
здесь надо рассмотреть два случая
1) х-5>0, x>5, тогда |x-5|=x-5 и 1/(х-5) -2<0, (1-2x+10)/(x-5) <0,
(11-2x)/(x-5) <0 , - __(5)+___(5,5)___-___
общее решение x>5,5 (с учетом, что x-5>0)
2) x-5<0, x<5, тогда |x-5|=5-x и получим уравнение:
1/(5-x) -2<0, (1-10+2x)/ (5-x) <0, (2x-9)/ (5-x) <0
-___(4,5)+(5)___- и общее решение
x<4,5 (с учетом, что x-5<0) , объединяем два случая и
ответ: (-Б; 4,5) и (5,5; +Б) (Б- бесконечность)