а) Точки, лежащие на оси Ox, имеют ординату, равную нулю. Значит, вторая координата вектора OM равна 0.
б) Точки, лежащие на оси Oy, имеют абсциссу, равную нулю. Значит, первая координата вектора OM равна 0.
в) Точки, лежащие в 1 четверти, имеют положительные абсциссу и ординату. Значит, координаты вектора OM положительны.
г) Точки, лежащие во 2 четверти, имеют отрицательную абсциссу и положительную ординату. Значит, первая координата вектора OM отрицательна, а вторая - положительна.
д) Точки, лежащие в 3 четверти, имеют отрицательные абсциссу и ординату. Значит, координаты вектора OM отрицательны.
е) Точки, лежащие в 4 четверти, имеют положительную абсциссу и отрицательную ординату. Значит, первая координата вектора OM положительна, а вторая - отрицательна.
я подозреваю что тут закралась неясность, в прогрессии насколько я помню количество элементов бесконечно, хотя в убывающей геометрической прогресии сумма всех элементов может сходиться.
инфми словами условие следует понимать так что n первых членов прогресии, где n = 2k,
выполняется условие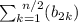 
в три раза больше, чем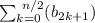 
рассмотрим это более подробно на примере первых шести элементов
сумма нечетных S(1,3,5) = b1 + b3 + b5
сумма четных S(2,4,6) = b2 + b4 + b6 = b1*q + b3*q + b5*q = q(b1 + b3 + b5) = q*S(1,3,5)
следовательно отношение между четной суммой и нечетной равно знаменателю прогрессии.
Для нашей задачи это число 3
ответ 3
S-путь; V-скорость; t1-время запланированное; t2-время проехали
t1=S/V
t2=(1.4S)/(1.6V)
t2/t1= ((1.4S)/(1.6V)) / (S/V)=1,4SV/1.6SV=1.4/1.6=0.875
t2/t1*100%=0.875*100=87.5%
100%-87.5%=12.5% На столько процентов время движения оказалось меньше запланированного