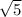Выносим х^2 как постоянный множитель, получаем:
х^2(x^2-5)=0
Произведение равно нулю, когда один из множителей равен нулю, а другой при этом существует:
x^2=0 или x^2-5=0
x=0 x^2=5
x1=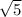
x2=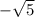
ответ:0, 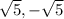
а). 16а³/5b•35b²/12a⁴= 16a³•35b²/5b•12a⁴=8•7b/6a=4•7b/3a
б). (7m-3)•m³/35m-15= (7m-3)•m³/5(7m-3)=m³/5
в). 6cd/c²-4c•c²-16/18d²=6cd•(c-4)(c+4)/c(c-4)•18d²= 6d(c+4)/18d²= c+4/3d
г). (-5х²/у³)²= 25x⁴/y6
Объяснение:
a). сначала умножаем числитель на числитель и знаменатель на знаменатель; потом упрощаем
б). умножаем разность на числитель (т.к. у этой разности знаменатель 1 и его просто не пишут), в знаменателе можно вынести 5, сокращаем все.
в). в 1 знаменателе можно вынести с, а во втором числители формула
г). степень после скобок относится ко всей дроби, так что возводим в степень 2 и числитель и знаменатель(- при этом уйдет, т.к. степень четная)
ответ:изи
Объяснение:
1. Длина окружности равна: L = 100 м;
2. Скорость первого тела: X м/сек;
3. Скорость второго тела: Y м/сек;
4. Встреча тел при движении в одну сторону происходит каждые: Td = 20 сек;
5. Разностная скорость тел: Vp = (X - Y) м/сек;
6. При движении в противоположные стороны время встречи: Tb = 4 сек;
7. Суммарная скорость тел: Vc = (X + Y) м/сек;
8. Составляем два уравнения:
Vp = X - Y = L / Td = 100 / 20 = 5 м/сек;
Vc = X + Y = L / Tb = 100 / 4 = 25 м/сек;
9. Складываем и вычитаем уравнения:
2 * X = 5 + 25 = 30;
X = 30 / 2 = 15 м/сек;
2 * Y = 25 - 5 = 20;
Y = 20 / 2 = 10 м/сек.
ответ: скорость первого тела 15 м/сек, второго 10 м/сек.
x^4-5x^2=0
x^2(x^2-5)=0
x^2=0 x^2=5
x=0 x= -+