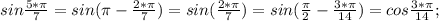
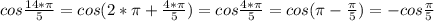
В решении.
Объяснение:
Используя график функции у = x² - 12x + 32, найдите решение неравенства x² - 12x + 32 ≥ 0.
Приравнять к нулю и решить квадратное уравнение:
x² - 12x + 32 = 0
D=b²-4ac =144 - 128 = 16 √D=4
х₁=(-b-√D)/2a
х₁=(12-4)/2
х₁=8/2
х₁=4;
х₂=(-b+√D)/2a
х₂=(12+4)/2
х₂=16/2
х₂=8;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= 4 и х= 8.
Решение неравенства: х∈(-∞; 4]∪[8; +∞).
Неравенство нестрогое, скобки квадратные, а знаки бесконечности всегда с круглой скобкой.
Составим уравнение. В левой его части запишем как вычисляется общая сумма проданного через число коробок, цену коробки (икс) и величину наценки (проценты прибыли). А в правой части будет эта самая общая сумма в шекелях, указанная в задании.
30x + 1,18*25x + 1,06*(60-30-25)*x = 6480
Решаем полученное уравнение:
30x + 29,5x + 1,06*5x = 6480
30x + 29,5x + 5,3x = 6480
64,8x = 6480
x = 6480 / 64,8 = 100 (шекелей) -цена одной коробки при покупке
Общая прибыль от продаж равна:
0,18*25x + 0,06*5x = 0,18*25*100 + 0,06*5*100 = 18*25 + 6*5 = 450 + 30 = 480 (шекелей)