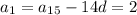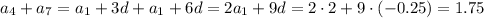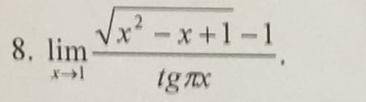

 Объяснение:1 Запишем
Объяснение:1 Запишем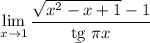
Представим 1 как дробь 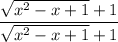
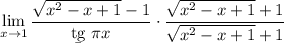
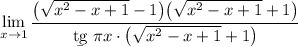 4 В числителе разность квадратов
4 В числителе разность квадратов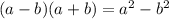 где
где
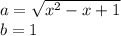
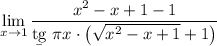
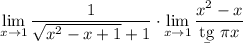 6 Можно посчитать первый предел
6 Можно посчитать первый предел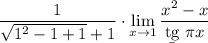
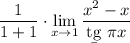
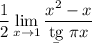
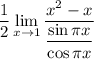 8 Вынесем косинус и посчитаем
8 Вынесем косинус и посчитаем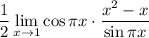
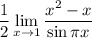 9 Разложим на множители числитель
9 Разложим на множители числитель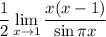
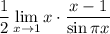
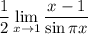 10 Умножим на 1
10 Умножим на 1Представим 1 как отношение 
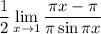
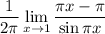
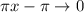 при
при 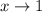
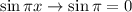 при
при 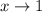
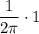
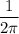
1. Б
Объяснение: Для умножения многочлена на многочлен существует очень легкое правило. Чтобы умножить два многочлена между собой, надо каждый член первого многочлена умножить на каждый член второго многочлена. После это полученные произведения сложить и привести подобные.
2. А
Объяснение: У вырази a*b е два множники, ''a''*b називається першим множником, а*''b'' називається другим множником.
3. В
Объяснение: Спрощуючи даний вираз, згрупуємо окремо числові та буквені множники.
4. Г
5. Б
Объснение: Коэффицие́нт «совместно» + «производящий») — термин, обозначающий числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.
6. А
1. Используя формулу n-го члена арифметической прогрессии: an = a1 + (n-1)d, решим следующую систему уравнений
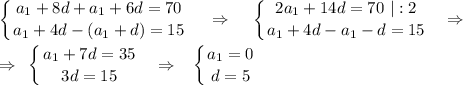
***************************************************************************************************
2. 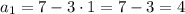
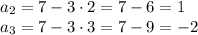
Имеем арифметическую прогрессию с первым членом 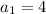 и разностью прогрессии
и разностью прогрессии 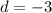
Сумма первых 12 членов арифметической прогрессии, равна:
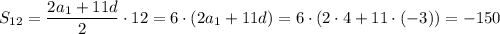
**************************************************************************************************
3. Разность прогрессии: 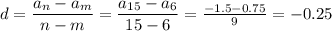
Первый член арифметической прогрессии: