История Украины — события на территории современной Украины с момента начала расселения людей и до сегодняшнего дня.
Первые поселения человека прямоходящего (Homo erectus) возникли на этой территории примерно 900—800 тысяч лет тому назад в рамках так называемой ашёльской культуры.
С V века до н.э. известно о хлебном экспорте из северного Причерноморья в Грецию. В IV веке н.э. в начале великого переселения народов степи северного Причерноморья занимаются тюркскими племенами. В VIII веке появляется плуг и массово возникают городища — укреплённые пункты местной знати.
С IX столетия в связи с освоением нового торгового пути «из варя́г в гре́ки» на его протяжении формируются новые союзы племён. В 860 году киевский князь Аскольд совершает первый поход на Византию. В 882 году после убийства киевских князей Олег становится правителем (регентом) при малолетнем князе Игоре. При Святославе власть киевских князей распространилась на все восточнославянские племена. При Владимире было принято христианство из Византии в качестве государственной религии (988[1]). При Ярославе Мудром (начиная с 1016 года) издан свод законов — Русская Правда. Права местных династий были признаны на Любечском съезде (1097), после 1132 года распад Киевской Руси стал необратимым.
Феодальная и политическая раздробленность сильно ослабили древнерусское государство. После монгольского нашествия 1237—1240 княжества оказались в зависимости от Золотой Орды.
В 1321 году литовский князь Гедимин в битве на реке Ирпень разбил объединённую армию южнорусских князей, после чего завоевал Киев, Переяславль, Белгород и другие ослабленные монгольским нашествием города. В 1362 году литовский князь Ольгерд, разбив армии Золотой Орды в сражении у Синих Вод, окончательно включает большую часть удельных княжеств до Чёрного моря в состав Великого княжества Литовского. Польское королевство захватило Галицкую и Холмскую земли (окончательно в 1387).
Объяснение:
В решении.
Объяснение:
Решить систему неравенств:
1) -4х <= -12
x + 2 > 6
Решить первое неравенство:
-4х <= -12
4x >= 12 знак меняется при делении на минус
х >= 3
Решение неравенства х∈[3; +∞).
Неравенство нестрогое, значение х=3 входит в интервал решений неравенства, скобка квадратная, а знаки бесконечности всегда с круглой скобкой.
Решить второе неравенство:
x + 2 > 6
х > 6 - 2
x > 4
Решение неравенства х∈(4; +∞).
Неравенство строгое, значение х=4 не входит в интервал решений неравенства, скобка круглая, а знаки бесконечности всегда с круглой скобкой.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения 3; 4; +∞.
х∈[3; +∞) - штриховка вправо от 3 до + бесконечности.
х∈(4; +∞) - штриховка вправо от 4 до + бесконечности.
Пересечение решений (двойная штриховка) от 4 до + бесконечности.
Решение системы неравенств: х∈(4; +∞).
2) 8 - х > 5
x - 7 <= 2
Решить первое неравенство:
8 - х > 5
-х > 5 - 8
-x > -3
x < 3 знак меняется при делении на минус
Решение неравенства х∈(-∞; 3).
Неравенство строгое, скобки круглые.
Решить второе неравенство:
x - 7 <= 2
х <= 2 + 7
х <= 9
Решение неравенства х∈(-∞; 9].
Неравенство нестрогое, скобка квадратная.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения -∞; 3; 9.
х∈(-∞; 3) - штриховка вправо от - бесконечности до 3.
х∈(-∞; 9] - штриховка вправо от - бесконечности до 9.
Пересечение решений (двойная штриховка) от - бесконечности до 3.
Решение системы неравенств: х∈(-∞; 3).
3) 3х - 3 < 5x
7x - 10 < 5x
Решить первое неравенство:
3х - 3 < 5x
3х - 5х < 3
-2x < 3
2x > -3 знак меняется при делении на минус
x > -1,5
Решение неравенства х∈(-1,5; +∞).
Неравенство строгое, скобки круглые.
Решить второе неравенство:
7x - 10 < 5x
7х - 5х < 10
2x < 10
x < 5
Решение неравенства х∈(-∞; 5).
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения -∞; -1,5; 5.
х∈(-1,5; +∞) - штриховка вправо от -1,5 до + бесконечности.
х∈(-∞; 5) - штриховка вправо от - бесконечности до 5.
Пересечение решений (двойная штриховка) от - 1,5 до 5.
Решение системы неравенств: х∈(-1,5; 5).
4) 2 - 3х < 4x - 12
7 + 3x >= 2x + 10
Решить первое неравенство:
2 - 3х < 4x - 12
-3x - 4x < -12 - 2
-7x < -14
7x > 14 знак меняется при делении на минус
x > 2
Решение неравенства х∈(2; +∞).
Неравенство строгое, скобки круглые.
Решить второе неравенство:
7 + 3x >= 2x + 10
3х - 2х >= 10 - 7
x >= 3
Решение неравенства х∈[3; +∞).
Неравенство нестрогое, скобка квадратная.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения 2; 3; +∞.
х∈(2; +∞) - штриховка вправо от 2 до + бесконечности.
х∈[3; +∞) - штриховка вправо от 3 до + бесконечности.
Пересечение решений (двойная штриховка) от 3 до + бесконечности.
Решение системы неравенств: х∈[3; +∞).
Сначала просто решим неравенство методом интервалов:
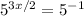 ;
;
Найдём корни числителя:
3x/2=-1;
x= -2/3;
Найдём корни знаменателя:
x-4=0;
x=4;
Теперь начертим числовую прямую, отметим на ней точки -2/3 и 4 и посмотрим, где всё выражение принимает значения больше нуля (числовая прямая прикреплена).
Мы видим, что всё выражение больше нуля при x>4 и x< -2/3
Поскольку нам нужен наименьшее целое положительное решение, мы берём число 5 (4 мы взять не можем, т.к. в знаменателе будет 0 и потому, что 4 не входит в получившиеся лучи).
ответ: 5.