P.S. Свойство верно только для . Но под знаком log в его аргументе может стоять квадрат какого-то выражения, т.к. квадрат любого выражения неотрицателен (больше или равен 0) . Из-за области определения логарифмической функции мы требуем , чтобы аргумент был строго больше 0, то есть остаётся, чтобы квадрат выражения не равнялся 0 . Во 2 (чётную) степень может возводится не только положительное, но и отрицательное выражение , а под знаком log должно остаться строго положительное выражение, поэтому в общем случае в аргументе log , надо писать модуль аргумента. Поэтому в общем случае действует свойство log , обведённое в рамочку.
Пусть r, h - радиус основания и высота цилиндра, R,H - радиус основания и высота конуса. Из подобия треугольников находим: r/(H-h) = R/H, откуда R = r*H/(H-h). Подставляем R в формулу для объема конуса: V = (1/3)*H*п*R^2 = (п/3)*r^2*H^3/(H-h)^2. Дифференцируем V по H: dV/dH = (п*r^2)*(H^2/(H-h)^2 - (2/3)*H^3/(H-h)^3)= =(п*r^2*H^2/(H-h)^2)*(1-(2/3)*H/(H-h)). Приравнивая производную нулю. Отбрасываем решение H=0 так как H>h, и находим экстремум при H = 3*h. Этот единственный экстремум должен соответствовать минимуму. То есть, объем описанного конуса минимален, когда высота конуса в три раза больше высоты цилиндра.
P.S. Свойство
верно только для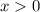 
. Но под знаком log в его аргументе может стоять квадрат какого-то выражения, т.к. квадрат любого выражения неотрицателен (больше или равен 0) . Из-за области определения логарифмической функции мы требуем , чтобы аргумент был строго больше 0, то есть остаётся, чтобы квадрат выражения не равнялся 0 . Во 2 (чётную) степень может возводится не только положительное, но и отрицательное выражение 
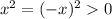, а под знаком log должно остаться строго положительное выражение, поэтому в общем случае в аргументе log , надо писать модуль аргумента. Поэтому в общем случае действует свойство log , обведённое в рамочку.