В решении.
Объяснение:
Задание 1.
Известно, что график функции f(x) проходит через точку (−5; 3) и параллелен графику функции y = −4x + 3.
а) Найдите уравнение данной функции f(x) ( ).
Графики линейных функций параллельны, если k₁ = k₂, а b₁ ≠ b₂.
k₁ = -4, значит, k₂ = -4;
Вычислить b₂:
Подставить в уравнение известные значения х и у (координаты точки) и вычислить b₂:
3 = -4 * (- 5) + b₂:
3 = 20 + b₂:
3 - 20 = b₂:
b₂ = -17;
Уравнение второй функции:
у = -4х - 17.
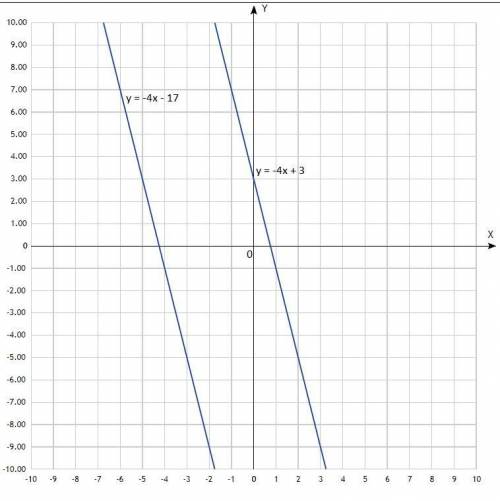
б) Постройте график данной функции f(x) ( ).
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
y = −4x + 3 у = -4х - 17
Таблицы:
х -1 0 1 х -6 -5 -4
у 7 3 -1 у 7 3 -1
По вычисленным точкам построить графики.
Объяснение:
1.а)6с
1.а)6с б)-15
2.a) 2a−6a 2 +4= 2a2(−3a+2)= a−3a+2
a) 2a−6a 2 +4= 2a2(−3a+2)= a−3a+2 b)\frac{- 7{x}^{3} + 14 {x}^{2} - 21x}{ - 7x} = \frac{ - 7x( {x}^{2} - 2x + 3) }{ - 7x} = x {}^{2} - 2x + 3b) −7x−7x 3
a) 2a−6a 2 +4= 2a2(−3a+2)= a−3a+2 b)\frac{- 7{x}^{3} + 14 {x}^{2} - 21x}{ - 7x} = \frac{ - 7x( {x}^{2} - 2x + 3) }{ - 7x} = x {}^{2} - 2x + 3b) −7x−7x 3 +14x 2 −21x = −7x−7x(x 2 −2x+3) =x 2 −2x+3
−2x+3) =x 2 −2x+3в)
−2x+3) =x 2 −2x+3в)\frac{ {9a}^{3} c -6 {a}^{2} {c}^{2} }{3 {a}^{2} {c}^{2} } = \frac{3 {a}^{2} {c}^{} (3 a - 2c)}{3a {}^{2} c {}^{2} } = \frac{3a - 2c}{c} то
3a 2 c 29a 3 c−6a 2 c 2 = 3a 2 c 23a 2 c (3a−2c)
23a 2 c (3a−2c)= c3a−2c
23a 2 c (3a−2c)= c3a−2c
3.на фотографии

Вероятность:
P(a) = m/n, где n - общее количество карт, m - "нужные" карты.
Туз пик - один во всей колоде. вероятность 1/33.
Валетов черной масти - 2 верояность 2/33
Общая вероятность вытащить равна сумме вероятностей.
2/33 + 1/33 = 1/11
ответ : 1 /11