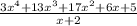
Пусть в стаде было x коров, т.к. количество коров в стаде увеличилось на 60, то их стало (х+60) коров
Удой молока с одной коровы был 12,8 л в день, следовательно от х коров в день получали 12,8х л молока
Удой возрос до 15л с коровы, т.о. от (х+60) стали получать 15*(х+60) л молока в день
Т.о. надои в день увеличились на 15(х+60)-12,8х, что по условию задачи равно 1340 л
Получим уравнение
15(х+60)-12,8х=1340
15х+900-12,8х=1340
2,2х=1340-900
2,2х=440
х=440/2,2
х=200
В стаде было 200 коров, следовательно стало 200+60=260 коров
ответ: 260 коров
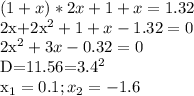
Объяснение: подсказка в знаменателе))
сгруппируем числитель так:
3x^4+6x^3 + 7x^3+14x^2 + 3x^2+6x + 5 = 3x^3(x+2) + 7x^2(x+2) + 3x(x+2) + 5 = (x+2)*(3x^3+7x^2+3x) + 5
теперь дробь можно представить в виде суммы двух дробей с одинаковым знаменателем... и в первой дроби общий множитель (х+2) сократится, а вторая дробь останется:
3x^3+7x^2+3x + (5 / (x+2))