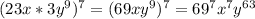
1)
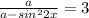

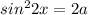
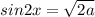
Так как значения синуса не могут быть большими единицы, получаем:

Так как выражение под радикалом и собственно весь радикал не могут быть отрицательными получаем:

Откуда получаем:
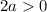

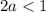
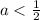
Объединяя полученные результаты получаем: a∈
ответ: a∈
2)

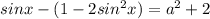


Получаем квадратное уравнение относительно t:

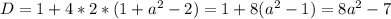


Исходя из того что данное уравнение должно иметь лишь одно решение получаем, что дискриминант должен быть равен нулю:
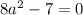
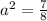
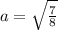
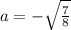
Но так как нам нужно только одно решение в заданном промежутке получаем:

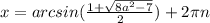

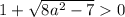
неравенство не имеет решений
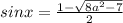


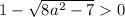

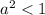
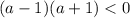
Получаем, что при a∈ данное уравнение имеет лишь один корень
данное уравнение имеет лишь один корень
ответ: a∈