
Объяснение:
Сначала найдём вероятность обратного события, а именно "обе извлечённые детали — не стандартны".
Всего нестандартных деталей 10 - 8 = 2 штуки. Соответственно, есть только один извлечь именно их.
Всего же извлечь две детали из 10 будет 10!/(2!(10-2)!) = 10!/(2!8!) = 10*9/2 = 45.
Таким образом, вероятность события "обе извлечённые детали — не стандартны" составляет 1/45.
Тогда вероятность искомого события равна 1 - 1/45 = 44/45.
ответ: вероятность того, что среди наудачу извлечённых двух деталей будет хотя бы одна стандартная, составляет 44/45.
Условие. Y²+xy-4x-9y+20=0 ; y=ax+1 ; x>2
найти все значения а, при которых графики имеют одну общую точку(в нашем случае (ax+1)² + x(ax+1) -4x - 9(ax+1)+20=0 имеет единственное решение).
Подставим у = (ax+1)² в уравнение у²+xy-4x-9y+20=0, получим
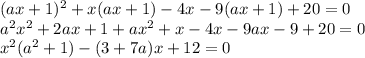
Найдем дискриминант квадратного уравнения относительно x
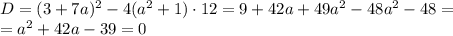
Получим 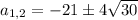
Если подставить 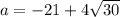 , т.е. имеется квадратное уравнение
, т.е. имеется квадратное уравнение  , у которого корень
, у которого корень
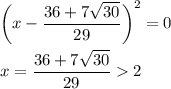
Если подставить  , т.е. имеется квадратное уравнение
, т.е. имеется квадратное уравнение 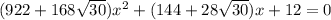 , у которого корень
, у которого корень
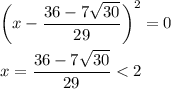
ответ: 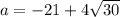
Объяснение:
3(х - 2) . (х + 3) - 3х² ∠ 4
3х + 5 ≥ 4х + 8
(3х - 6) . (х + 3) - 3х² ∠ 4
3х - 4х ≥ 8 - 5
3х² + 9х - 6х - 18 - 3х² ∠ 4
-х ≥ 3
3х ∠ 4 + 18
х ≤ -3
3х ∠ 22
х ≤ -3
х ∠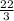
х ≤ -3
б)