ОТВЕТ: 1/15.
Решение Пусть событие А - оба шара черные.
Воспользуемся классическим определением вероятности. Вероятность события А найдем как отношение числа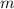 
благоприятных исходов к числу 
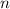всех возможных исходов: 
.
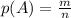Всего шаров 7 + 3 = 10. Выбрать 2 шара из 10 - поскольку не учитывается порядок - можно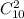 
поэтому
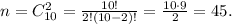
Выбрать 2 черных шара из 3 можно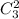 
поэтому
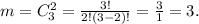
Итого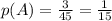 
Разобьем событие как бы на два других: В - первый шар будет черным; С - второй шар будет черным.
Вероятность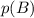 
того, что первый шар будет черным, по определению вероятности равна 
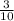, поскольку всего шаров 10, а черных - 3. После того, как взяли один черный шар, всего осталось 9 шаров, из которых 2 черных. Поэтому вероятность 
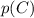того, что второй шар будет черный, равна 
.
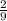Поскольку необходимо, чтобы одновременно и первый, и второй шар были черными, искомую вероятность можно найти, перемножив вероятности событий В и С, т.е.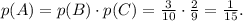 
ответ: №1 х>8,5 №2 46°, 46°, 88° или 46°, 67°, 67°
Объяснение: №1 Пусть х см-1 сторона, тогда (х-5) см -2 сторона. По неравенству треугольника каждая сторона должна быть меньше суммы двух других сторон треугольника, ⇒ треугольник существует, если 12 < x +(x-5) ⇒ 17 < 2x ⇒ x>8,5 №2 Пусть дан ΔАВС -равнобедренный, причём ∠А и∠С-углы при основании. Возможны 2 случая: 1) если ∠А=46°, то ∠С=∠А=46°(как углы при основании равноб треуг)⇒∠В=180°- (46°+46°)=88°; 2) Если ∠В=46°, то ∠А=∠С= (180°-46°):2 =67°