Функция
y = cos²(3x² + 1)
Первая производная функции
у' = 2cos(3x² + 1) · (-sin(3x² + 1)) · 6x
у' = - 6x · 2cos(3x² + 1) · sin(3x² + 1)
у' = - 6x · sin(6x² + 2)
Вторая производная функции
y'' = -6 · sin(6x² + 2) - 6x · cos(6x² + 2) · 12x
y'' = -6 · sin(6x² + 2) - 72x² · cos(6x² + 2)
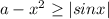
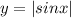расположен выше оси ОХ. 
.
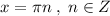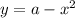- это параболы , ветви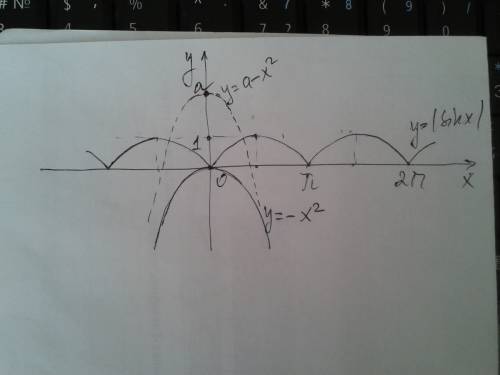
ответ:
cost=(x–2)/3
{sint=(y–3)/2
возводим в квадрат и складываем
это эллипс.
(x–2)2/9+(y–3)^/4=1
этот эллипс равновелик эллипсу
(x2/9)+(y2/4)=1
параметрическое уравнение которого
{x=3cost
(y=2sint
[0; 3] на оси ох получаем
если t1=π/2 и t2=0
в силу симметрии достаточно вычислить четвертую часть искомой площади, результат умножить на 4.
s=4·∫0π/2 y(t)·xtdt=
= –4∫π/2 0 (2sint)·(–3sint)dt= 24∫π/2 0 (sin2t)dt=
= 24∫π/2 0 (1–cos2t)/2dt=
=12t|π/2 0 –(3sin2t)|π/2 0 =6π
По идеи - 72*x^2*cos(1 + 3*x^2)^2 + 72*x^2*sin(1 + 3*x^2)^2
Объяснение: