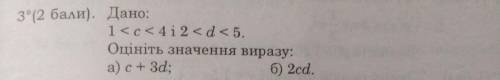
ответ: 1) x = (a + b) / (a - b); a ≠ b; 2) x = 2 · (m - n); 3) x = a + 1;
4) x = (3 · (m - n)) / (m + n); m ≠ - n
Объяснение:
1) a²x - b²x = a² + 2ab + b²; x · (a - b) · (a + b) = (a + b)²; x = (a + b)² / (a - b) · (a + b)
x = (a + b) / (a - b); a ≠ b
2) 3mx + 3nx = 6m² - 6n²; 3 · x · (m + n) = 6 · (m + n) · (m - n);
x = (6 · (m + n) · (m - n)) / 3 · (m + n); x = 2 · (m - n)
3) ax + x = a² + 2a + 1; x · (a + 1) = (a + 1)²; x = (a + 1)² / (a + 1) = a + 1; x = a + 1
4) m²x + 2mnx + n²x = 3m² - 3n²; x · (m + n)² = 3 · (m + n) · (m - n);
x = (3 · (m + n) · (m - n)) / (m + n)²; x = (3 · (m - n)) / (m + n); m ≠ - n
По условию получаем систему уравнений (если х×у=-75), то:
1-е число-х
2-е число-у
{х+у=20
{х×у=-75
х=(20-у)
(20-у)×у=-75
-у²+20у=-75
у²-20у-75=0
D=(-(-20))²-4×1×(-75)=400+300=700
у1=(-(-20)-√700)/2×1=(20-√700)/2=(20-26,46)/2=-6,46/2=-3,23
у2=(-(-20)+√700)/2×1=(20+26,46)/2=46,46/2=23,23
х1=20-y1
x1=20-(-3,23)
x1=23,23
x2=20-y2
x2=20-23,23
x2=-3,23
проверка: х1×у1=-75
23,23×(-3,23)=-75
-75,0329≈-75
ответ: (23,23;-3,23) и (-3,23;23,23)
если (х×у=75), то
{х+у=20
{х×у=75
х=(20-у)
(20-у)×у=75
20у-у²=75
у²-20у+75=0
D=(-(-20))²-4×1×75=400-300=100
y1=(-(-20)-√100)/2×1=(20-10)/2=10/2=5
y2=(-(-20)+√100)/2×1=(20+10)/2=15
x1=20-y1
x1=20-5
x1=15
x2=20-y2
x2=20-15
x2=5
ответ: (15;5) и (5;15).
Объяснение:
а) с+d
3<c+d<9
б) 2cd
4<2cd<40
a) c+3d
7<c+3d<19