через 180 минут
Объяснение:
Первый раз поравняется примерно в 9-50. На самом деле чуть раньше, но это не важно, потому что это время все равно компенсируется на следующих оборотах.*
Значит первый раз через примерно 50 минут (в 9-50)
второй раз примерно через 65 минут (в 10-55)
третий раз снова через 65 минут (ровно в 12 часов)
Итак 50+65+65=180 минут
Можно и по другому. Стрелки встречаются 1 раз в час. В 9-00 они уже не встретились. Значит три раза они встретятся через три оборота минутной стрелки, то есть ровно в 12-00, через три часа.
3 часа=180 минут
*компенсируется время - подразумевается что первый раз она может поравняться не ровно в 9-50, а допустим в 9-49, потому что часовая стрелка еще не встанет ровно на 10, но тогда следующий круг минутная пройдет не 65 минут, а 66, потому сумма не изменится. А когда дойдет до третьего раза в 12 часов то стрелки совпадут точно.
Выделим полный квадрат:
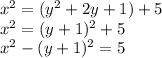
Раскладываем левую часть по формуле разности квадратов:
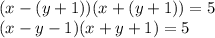
5 можно разложить в произведение двух сомножителей следующими
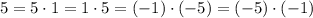
Это позволяет заменить рассмотрение уравнение на совокупность из четырёх систем:
1) x - y - 1 = 5, x + y + 1 = 1
Складываем и вычитаем уравнения:
2x = 5 + 1, 2y + 2 = 1 - 5
x = 3, y = -3
2) x - y - 1 = 1, x + y + 1 = 5
2x = 1 + 5, 2y + 2 = 5 - 1
x = 3, y = 1
3) x - y - 1 = -1, x + y + 1 = -5
2x = -1 - 5, 2y + 2 = -5 + 1
x = -3, y = -3
4) x - y - 1 = -5, x + y + 1 = -1
2x = -5 - 1, 2y + 2 = -1 + 5
x = -3, y = 1
Этот же ответ можно было получить из первого решения и того, что если (x, y) – решение, то и (-x, y) и (x, -2 - x) – решение.
ответ. (3, -3), (3, 1), (-3, -3), (-3, 1)
это замечательный предел
lim при x->0=sin2x sinx\x во 2 степени=lim при x->0=sin2x/2x *2*lim при x->0sinx/x=2*1=2