x^4-17*x^2+16 = 0
Пусть x^2= t, тогда
t^2- 17t+ 16= 0
17+-√289-64
t=
2
17+-√225
t=
2
17+-15
t=
2
t= 1
t= 16
Решим квадратное уравнение, где x^2= t. Получим
x^2= 1 и x^2= 16
х= 1 х=4
х= -1 х =-4
ответ: 1, -1, 4, -4
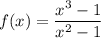
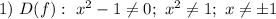
Следовательно, 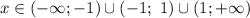
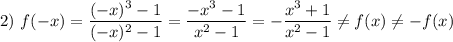 , значит, функция ни четная, ни нечетная; непериодическая.
, значит, функция ни четная, ни нечетная; непериодическая.
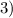 Если
Если 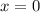 , то
, то 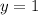 , значит (0; 1) — точка пересечения с осью ординат. Если
, значит (0; 1) — точка пересечения с осью ординат. Если 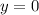 , то есть
, то есть 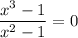 , то
, то 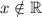 . Таким образом, функция не имеет точек пересечения с осью абсцисс.
. Таким образом, функция не имеет точек пересечения с осью абсцисс.
Значит, (0; 1) — единственная точка пересечения графика функции с осями координат.
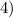 Поскольку
Поскольку 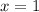 и
и 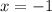 — точки разрыва функции и
— точки разрыва функции и 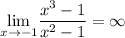 и
и 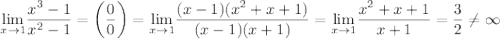 , то
, то 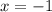 — вертикальная асимптота.
— вертикальная асимптота.
Если 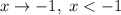 , то
, то 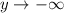 ; если
; если 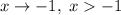 , то
, то 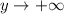 .
.
Найдем наклонные асимптоты 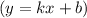 :
:
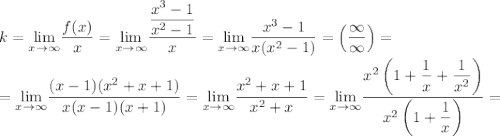
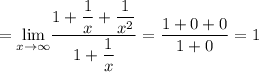
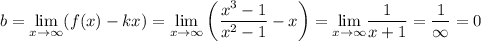
Следовательно, 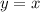 — наклонная асимптота.
— наклонная асимптота.
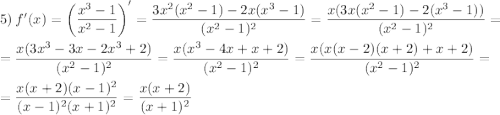
Найдем критические точки, приравняв первую производную к нулю: 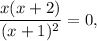 откуда
откуда 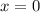 и
и  .
.
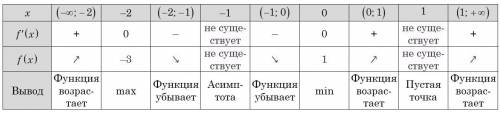
Заполним таблицу №1 (см. вложение).
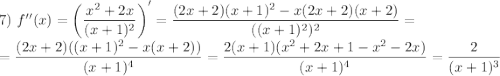
Если 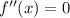 , то есть
, то есть 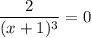 , то
, то 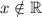 , значит, нет точек перегиба.
, значит, нет точек перегиба.
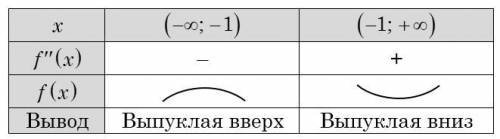
Систематизируем данные, полученные по второй производной, в таблицу №2.
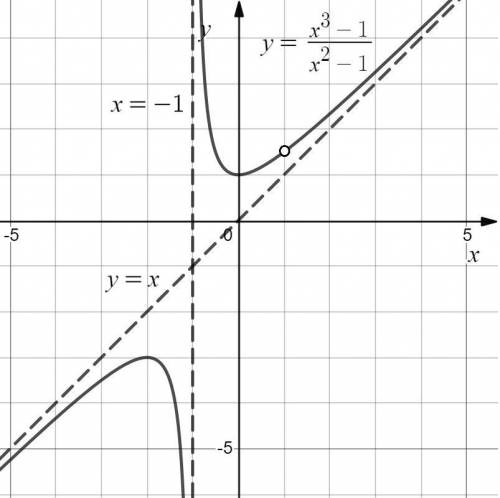
 График функции изображен на рисунке (см. вложение).
График функции изображен на рисунке (см. вложение).
 Из графика делаем вывод:
Из графика делаем вывод:
![E(f): \ y \in (-\infty; -3] \cup [1; +\infty)](/tpl/images/1059/8179/fda75.png)
тааак...
заменяем х^2=a, получаем...
а^2-17a+16=0
a1+a2=17
a1*a2=16
по т. Виета a1 = 16, a2 = 1
x^2=16 х^2=1
x=+4,-4 x=-1,+1
-4-1+1+4=0
Вроде все верно)