Sin^2x+2sinx*cosx-3cos^2x+2=0

Question

Алгебра: Sin^2x+2sinx*cosx-3cos^2x+2=0

Matveyka16 · Accepted Answer

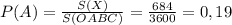
Решим задачу, используя геометрическую вероятность.

Пусть $x,y\in[0;\ 60]$ - минута прибытия первого и второго.

Встреча произойдет, если выполнится условие: 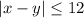$|x-y|\leq 12$ . Перепишем условие в виде:

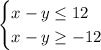
$\begin{cases} x-y\leq 12\\ x-y\geq -12\end{cases}$

$\begin{cases} y\geq x-12\\ y\leq x+12\end{cases}$

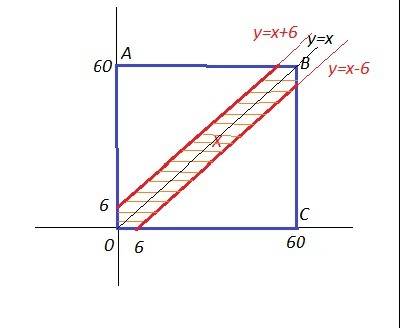
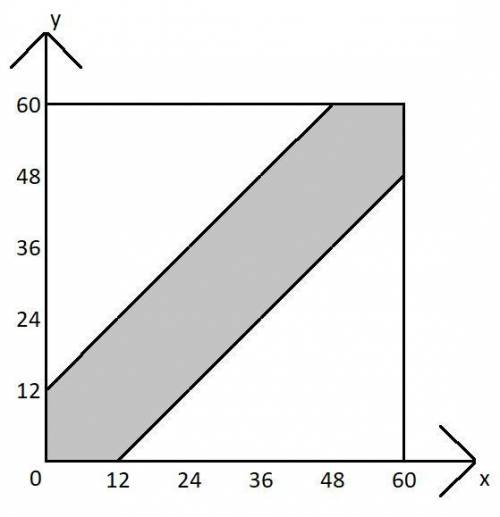
Изобразим графически это условие - получим шестиугольник. Его площадь соответствует благоприятным исходам.

Общая площадь - площадь квадрата - соответствует всем возможным исходам.

Отношение площади шестиугольника к площади квадрата и даст искомую вероятность.

Площадь шестиугольника найдем как разность между площадью квадрата и площадью двух незакрашенных треугольников.

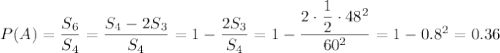
$P(A)=\dfrac{S_6}{S_4} =\dfrac{S_4-2S_3}{S_4} =1-\dfrac{2S_3}{S_4} =1-\dfrac{2\cdot\dfrac{1}{2}\cdot48^2}{60^2} =1-0.8^2 =0.36$

ответ: 0.36