
Если уравнение делить на cosx, то надо оговориться, что 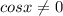 , так как на 0 делить нельзя. В силу этого можно потерять корни уравнения, при которых cosx обращается в 0, это
, так как на 0 делить нельзя. В силу этого можно потерять корни уравнения, при которых cosx обращается в 0, это 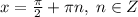 . Тогда надо отдельно проверить, не являются ли
. Тогда надо отдельно проверить, не являются ли 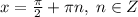 корнями заданного уравнения, подставив их в это уравнение.
корнями заданного уравнения, подставив их в это уравнение.
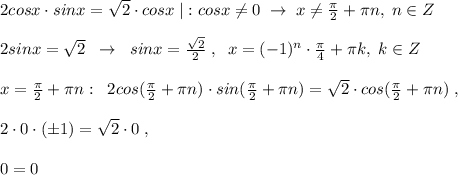
Так как получили верное равенство, то 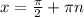 являются корнями заданного уравнения.
являются корнями заданного уравнения.
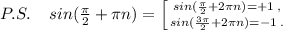
Чтобы не проводить лишнюю проверку , при решении уравнения надо просто вынести общий множитель cosx за скобку, тогда сразу получим две серии решений:
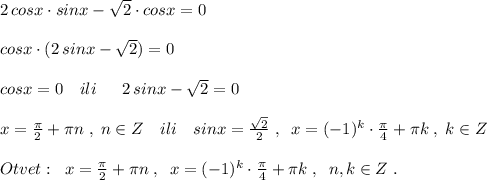
1) Пусть ВС=5 и AD=17 - основания трапеции. Тогда АВ=8 и СD=8 - ее боковые стороны.
2) Тогда, опустим перпендикуляры из точек В и С к оснвоанию АD. Они будут высотами.
3) АВ=СD=8 => АВСD - равнобедренная трапеция.
4) ABCD - равнобедренная трапеция
ВН⊥АD
СК⊥AD
Из всего вышеперечисленного в пункте следует, что HK=BC=5
5) AH=КD = (AD-HK):2 = (17-5):2=6
6) ΔABH - прямогульный => (По теореме Пифагора): АВ²=AH²+BH²
BH²=AB²-AH²
BH²=8²-6²
BH=5,29
8) Sabcd= 1/2ВН(ВС+АD)=1/2*5,29*22=58,19
ответ: 58,19.
ответ:10 часов 15 минут
Ну для начала смотрим, что отец и сын встретились на расстоянии 12 км от Кальтухи, отец же выехал из Кальтухи, значит отец проехал 12 км
А сын проехал:1) 30,75км - 12км = 18,75 км
2)узнаем сколько часов ехал Эмиль для этого расстояние делим на скорость: 18,75 : 15км/ч = 1(ч) 15(м)
3)10ч + 1ч 15м= 11(ч) 15(м)- это во столько они встретились
4)Узнаем сколько по времени ехал отец: 12км : 12км/ч = 1(ч)
5)А теперь, на сколько позже выехал отец: 1ч 15 м - 1ч = 15м
6)10ч(во столько выехал Эмиль)+ 15 минут(на столько позже выехал отец)=10ч 15 м: в это время выехал отец из Кальтухи.
Вроде бы так) Удачи