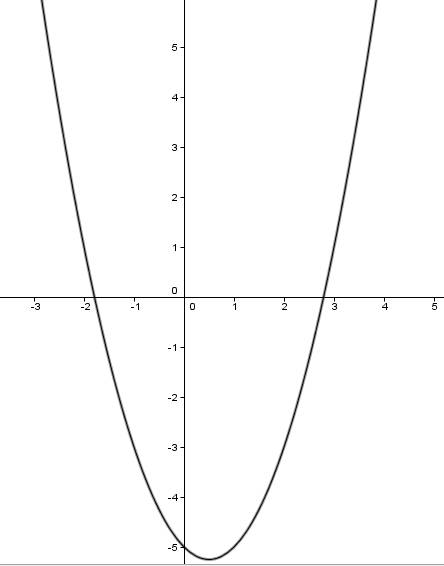
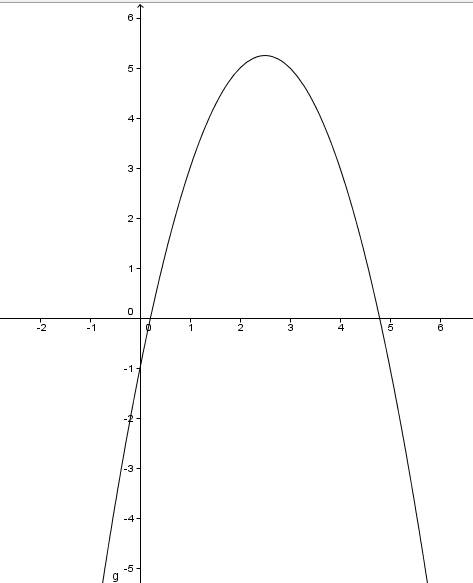
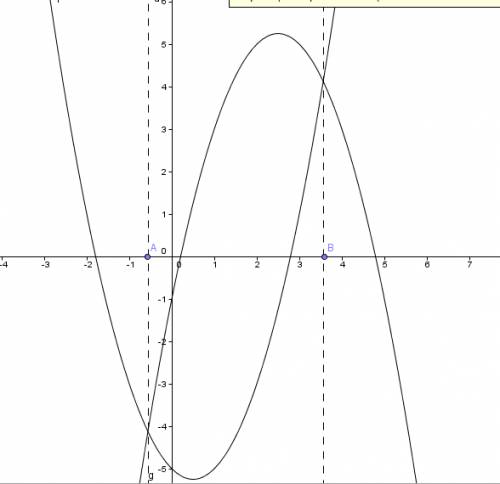
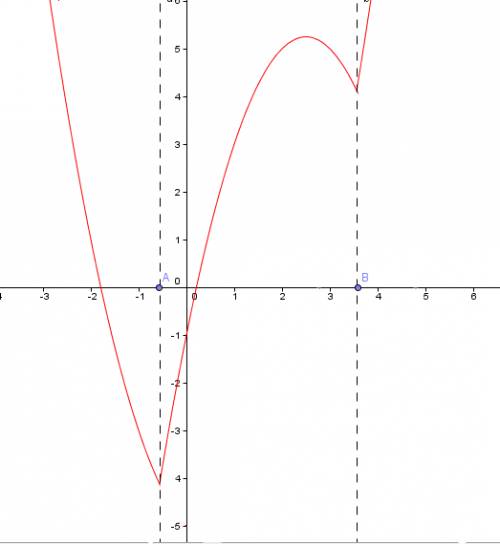
Дано неравенство ((2x-3) / (x^2+2x)) > 0,125 или ((2x-3) / (x^2+2x)) > 1/8.
Умножим обе части на 8: (16x - 24) / (x^2+2x) > 1.
По свойству дроби числитель больше знаменателя:
(16x - 24) > (x^2+2x). Перенесём левую часть вправо.
Получим равносильное неравенство x^2 + 2x - 16х + 24 < 0 или
x^2 - 14х + 24 < 0. Д = 196 - 4*24 = 100.
х1 = (14 + 10)/2 = 12, х2 = (14 - 10)/2 = 2.
Исходное неравенство можно представить так:
(х - 12)(х - 2)/(х(х + 2)) < 0.
Используем метод интервалов: -2 0 2 12
+ - + - +
Отсюда ответ: -2 < x < 0; 2 < x < 12.
1) y ' =-корень из х+ (12-x)/2корень из х=(-3x+12)/2корень из х =0, х=4
Теперь вычислим значения функции в точках х=1; 4; 9
y(1)=11; y(4)=16; y(9)=9. Значит, наибольшее значение у=16, наименьшее у=9
2) y ' =(1/3)*(-3sin3x)=-sin3x=0, 3x=Пn, x=Пn/3. В данный промежуток попадает
x=П/3. Найдем значения функции.
y(0)=1/3; y(П/3)=(1/3)*cosП=-1/3; y(П/2)=(1/3)*cos(3п/2)=0
Отсюда: наибольшее значение у=1/3, наименьшее у=-1/3