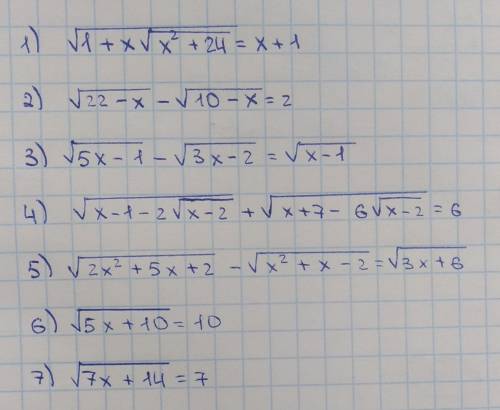
чтобы решить это уравнения надо построить в одной координатной плоскости графики функций y=sqrt(x) и y=6-x , абсцисса точки пересечения этих графиков и будет корнем этого уравнения
1) y=sqrt(x) - график этого уравнения - лежачая полупарабола, определенная только при значении x>=0
находим некоторые точки:
x=0; y=0; (0;0)
x=1; y=1; (1;1)
x=4; y=2; (4;2)
2) y=6-x - линейная функция, график - прямая линия
находим некоторые точки:
x=0; y=6 (0;6)
x=6; y=0; (6;0)
график в приложении:
красным цветом - график y=sqrt(x)
синим цветом - график y=6-x
эти функции пересекаются в точке (4;2)
откуда x=4
ответ: x=4
Объяснение:
1)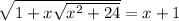
x₁ = 0, x₂ =5
2)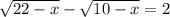
x=6
3)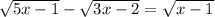
x=2