Не могу понять ,зачем решать графически ,когда эта интерпретация и есть аналитическое решение ,только в другой форме?
Причём в такой форме ,что не является обоснованным доказательством нашего корня или чего-нибудь другого
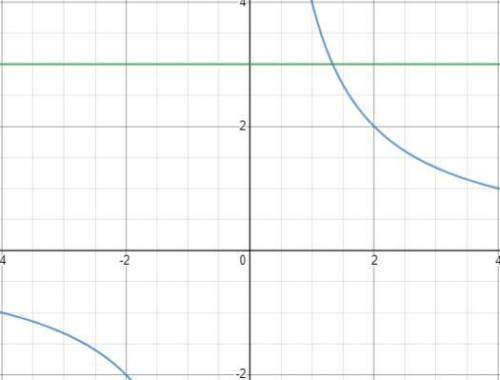
В первом ,да и как во втором уравнении ,у нас справа обратная пропорциональность
Первое уравнение!
Так как ,число а>0 в нашем случаи это 4 ,то функция располагается в первой и третьей четвертях
Так как у нас константа 3 ,то решение будет одно!
Так как просят решить графически ,то ссылаясь на один корень ,то он просто угадывается и это 4/3
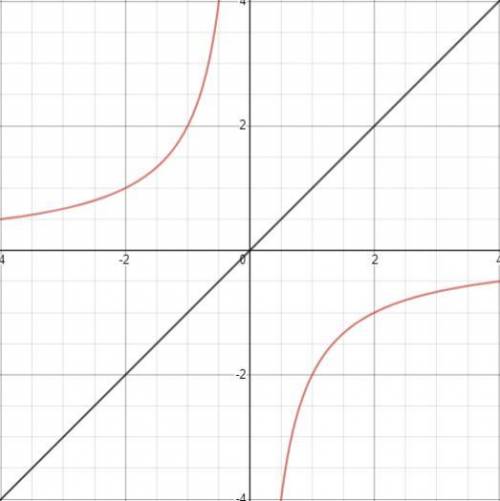
Второе уравнение!
Так как ,число a<0 в нашем случаи это -2,то функция будет располагаться во второй и четвёртой четвертях
Но как можно видеть,слева у нас f(x)=x - прямая
Данная прямая располагается в первой и четвёртых четвертях,так как a>0 ,следовательно данное уравнение не имеет решений!
х ВГ
ДДЕЕ
После долгих мучений... Обращаем внимание на произведение ДДЕЕ, оно делится на 11. Число делится на 11, если сумма цифр, которые стоят на чётных местах равна сумме цифр, стоящих на нечётных местах, либо отличается от неё на 11. На чётных местах стоят Д и Е, на нечётных тоже Д и Е. Следовательно, число ДДЕЕ делится на 11.
Теперь смотрим на множители. Хотя бы один из них должен тоже делиться на 11, иначе их произведение не разделится на 11. Ни АБ, ни ВГ не делятся на 11 по признаку делимости на 11.
Итак, множители не делятся на 11, а их произведение - делится. Так не бывает. Отсюда вывод, что ребус не имеет решения, разных ответов равно нулю.