
![-6\leq \frac{5-2x}{3}\leq2\\\\-6*3\leq \frac{5-2x}{3}*3\leq2 *3\\\\-18\leq5-2x\leq 6\\\\-18-5\leq5-2x-5\leq 6-5\\\\-23\leq-2x\leq1\\\\-0,5\leq x \leq11,5\\\\Otvet:\boxed{x\in[-0,5;11,5]}](/tpl/images/1476/8113/61fc6.png)
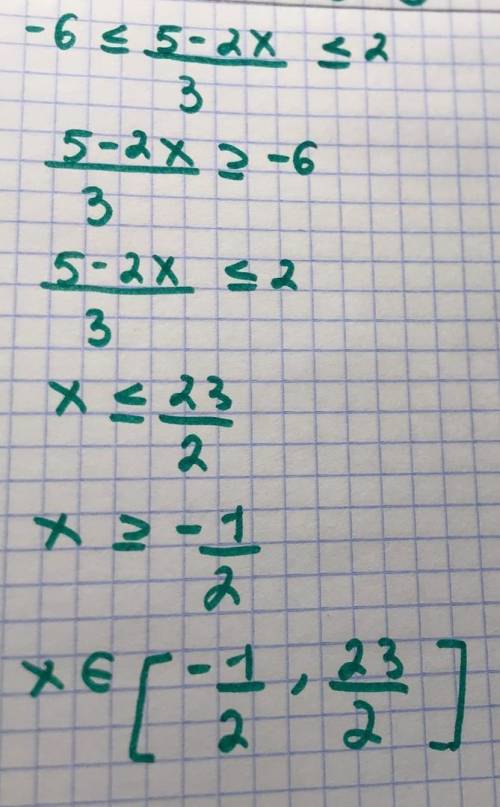
Данный ответ представлен фотографией.
Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).
Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегментом, а часть кривой, находящаяся между двумя крайними точками хорды называется дугой. В случае с замкнутыми кривыми (например, окружностью, эллипсом) хорда образует пару дуг с одними и теми же крайними точками по разные стороны хорды. Хорда, проходящая через центр окружности, является её диаметром. Диаметр — самая длинная хорда окружности.
Диа́метр в изначальном значении термина — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
r-радиус
D-диаметр
L-длина окружности
число пи(p)-3,14
L=pD=2pr - Это формула сразу и через диаметр, и через радиус.
Радиус окружности — отрезок, соединяющий любую её точку с центром.
3х-у=3, 2. 2х-3у=1, 3. 2х+у=1, 4. х+у=6,
3х-2у=0. 3х+у=7. 5х+2у=0. 5х-2у=9.
5. х+5у=7, 6. х+у=7, 7. 4х-3у=-1, 8. х+2у=-2,
3х+2у=-5. 5х-7у=11. х-5у =4. 3х-у=8.
9. 2х-5у=-7, 10. х-у=3, 11. 3х-5у=16, 12. 2х+3у=-7,
х-3у=-5. 3х+4у=2. 2х+у=2. х-у=4.
13. 2х+5у=-7, 14. х-3у=8, 15. 2х-3у=5, 16. х-4у=-1,
3х-у=15. 2х-у=6. х-6у=-2. 3х-у=8.
17. 5х-4у=12, 18. 6х+у=5, 19. 2х-3у=11, 20. х-6у=-2,
х-5у=-6. 2х-3у=-5. 5х+у=2. 2х+3у=11.
21. 3х-2у=16, 22. 2х+3у=3, 23. 4х-2у=-6, 24. 3х+2у=8,
4х+у=3. 5х+6у=9. 6х+у==11. 2х+6у=10.
25. 5х+у==14, 26. 3х-2у=5, 27. х+4у=7, 28. 2х-3у=5,
3х-2у=-2. 2х+5у=16. х-2у=-5. 3х+2у=14.
29. х-2у=7, 30. 4х-6у=26, 31. х+3у=7, 32. 8х+3у=-21,
х+2у=-1. 5х+3у=1. х+2у=5. 4х+5у=-7.
33. х-2у=8, 34. 8х+2у=11, 35. 2х-у=13, 36. 7х+3у=1,
х-3у=6. 6х-4у=11. 2х+3у=9. 2х-6у=-10.
37. 2х+3у=10, 38. 3х-2у=5, 39. 2х+у=-5, 40. 2х+3у=1,
х-2у=-9. 5х+4у=1. х-3у=-6. 6х-2у=14.