Смотри...................
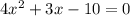, если их несколько, то указать сумму. 
): 
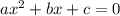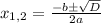, дискриминант же расписывается по-своему: 
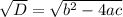. Дискриминант как бы заслужил своё отдельное внимание, ведь именно при его вычислении люди нередко допускают ошибки. Теперь – решаем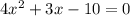, отсюда: 
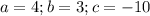, значит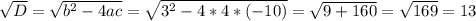
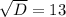; это как в алгебраических выражений седьмого класса – ты складываешь буквы, подставляешь вместо них какие-то числа и считываешь ответ, так вот здесь тоже самое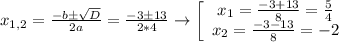
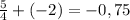
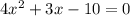равна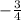 
Для начала нужно найти производную функции:
y'=-2x+6 (по табличному значению квадратной функции)
Далее находим нули функции, приравняв y к нулю. В данном случае он один: x=3
Строим числовую прямую и указываем на ней 3. Получаем два промежутка. При любом значении из (-∞, 3] функция возрастает, а на [3; +∞) - убывает. Следовательно число 3 - максимум.
Подставляем максимум вместо аргумента и получаем наибольшее значение:
-(3)^2+6*3-5=-9+18-5=4
ответ:4
Объяснение: