
Объяснение:
1а) х₁х₂=20=20×1=2×10=4×5
х₁+х₂=9=4+5⇒х₁=4; х₂=5
1б) х₁х₂=-12=-12×1=-2×6=-4×3
х₁+х₂=-11=-12+1⇒х₁=-12; х₂=1
1в) х₁х₂=-56=-56×1=-2×28=-4×14=-8×7
х₁+х₂=-1=-8+7⇒х₁=-8; х₂=7
1г) х₁х₂=88=88×1=2×44=4×22=8×11
х₁+х₂=19=8+11⇒х₁=8; х₂=11
2а) х₁х₂=63=63×1=3×21=9×7
х₁+х₂=-16=-9-7⇒х₁=-9; х₂=-7
2б) х₁х₂=-48=-48×1=-2×24=-4×12=-8×6=-16×3
х₁+х₂=-2=-8+6⇒х₁=-8; х₂=6
3) х₁+х₂=12
х₁-х₂=2
2х₁=14⇒х₁=7⇒х₂=12-7=5⇒q=х₁х₂=7×5=35
4) х₁+х₂=-1
х₁-х₂=6
2х₁=5⇒х₁=2,5⇒х₂=-1-2,5=-3,5⇒c= х₁х₂=-2.5×3,5=-8,75
5) х₁²-х₂²=12⇒( х₁+х₂)( х₁-х₂)=12⇒-2( х₁-х₂)=12⇒ х₁-х₂=-6
х₁+х₂=-2
х₁-х₂=-6
2х₁=-8⇒ х₁=-4⇒ х₂=-2+4=2⇒q= х₁х₂=-8
ответ: (2; 3)
Объяснение:
Решить графически уравнение:
Построим два графика
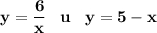
Абсциссы точек пересечения этих графиков будут решением данного уравнения.1.
- функция обратной пропорциональности, график - гипербола.
Построим ветвь гиперболы:
Вторую ветвь строим симметрично относительно начала координат.
2.
- линейная функция, график - прямая.
Для построения прямой достаточно двух точек:
3. Построили графики.
Точки пересечения:
А (2; 3) и В (3; 2)
Решением уравнения будут абсциссы этих точек пересечения, то есть (2; 3).