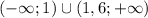1) Обозначим искомую линейную функцию у = kx +b. По условию её график параллелен прямой y=2x+11, следовательно угловые коэффициенты этих функций равны => k = 2 => искомая функция принимает вид у = 2x +b. 2) По условию график искомой функции пересекается с графиком y=x-3 в точке, лежащей на оси ординат, значит функции у = 2x +b, y=x-3 и ось ординат OY, которая задается формулой x = 0 пересекаются в одной точке. Решаем систему: у = 2x +b y=x-3 x = 0
Получаем: b = - 3. T.о. искомая функция имеет вид: у = 2x - 3
Сначала выразим tg(3a) через tg(a) Получили Мы знаем, что tg(a) - целое. Если tg(3a) тоже целое, то 3-tg^2(a) делится нацело на 1-3tg^2(a).
Ясно, что при tg a = 0 будет tg 3a = 0 Далее, например, при tg(a) = 1 получаем tg(3a) = 1*(3 - 1)/(1 - 3)= 1*2/(-2) = -1 А при tg(a) = -1 получаем tg(3a) = -1*(3 - 1)/(1 - 3) = (-1)*2/(-2) = 1 Но уже при tg(a) = 2 мы получаем tg(3a) = 2*(3 - 4)/(1 - 3*4) = 2*(-1)/(-11) = 2/11 Соответственно, при tg(a) = -2 мы получим tg(3a) = -2/11. Это уже нецелые значения, и ни при каких других а целых не будет. ответ: (0; 0); (1; -1); (-1; 1)
1) x^2+0.5x-14=0
D=0,5^2+4*14=56,25
x1=(-0,5+7,5)/2=3,5 x2=(-0,5-7,5)/2=-4
ответ: 3,5 и -4
3) x^2-2.6x+1.6>0
Решаем методом интервалов
x^2-2.6x+1.6=0
D=(-2,6)^2-4*1,6=0,36
x1=(2,6+0,6)/2=1,6 x2=(2,6-0,6)/2=1
Чертим координатную прямую, отмечаем точки, разбиваем на промежутки, определяем знаки(+, -, +).
х принадлежит