Найдите диагональ прямоугольника наибольшей площади, вписанного в прямоугольный треугольник с катетами 18 и 24, и имеющий с ним общий прямой угол. пишите все подробно,(оптимизирующую величину,уравнение с
производной и т.д) в 3 этапа или хотя бы 2

👇

Ответ:

ЛАЙФСТААААААЙЛ

13.05.2020

применено: пропорциональность сторон подобных треугольников, формула производной, зависимость поведения функции от знака производной, теорема Пифагора

Найдите диагональ прямоугольника наибольшей площади, вписанного в прямоугольный треугольник с катета

4,6(52 оценок)

Открыть все ответы

Ответ:

владик4441

13.05.2020

y=-x^2+2x+3

Найдем точки пересечения параболы с осью OX

-x^2+2x+3=0

x^2-2x-3=0

D=b^2-4ac=16

x1=3

x2=-1

S=int (-x^2+2x+3)dx от -1 до 3 = (-x^3/3+x^2+3x ) от -1 до 3 = 9-(-1 2/3)=10 2/3

2) y=-2*(x-3)^2+2

Найдем точки пересечения параболы с осью OX

-2*(x-3)^2+2=0

Сделаем замену t=x-3

-2t^2+2=0

t^2=1

t1=1

t2=-1

То есть

a) x-3=1 => x=4

б) x-3=-1 => x=2

тогда

s= int(-2*(x-3)^2+2)dx от 2 до 4 =(-2*(x-3)^3/3 +2x) от 2 до 4 =22/3 - 14/3 = 8/3 = 2 2/3

4,8(73 оценок)

Ответ:

dan355

13.05.2020

Сначала нужно выполнить чертеж (смотрите рисунок). Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы y=4-x² и прямой y=2-x. Это можно сделать двумя
Первый это посмотреть на график где линии пересекаются, второй это аналитический В данном случае можно воспользоваться графическим так как на графике ясно видно, что парабола и прямая пересекаются в точке (-1 ; 3) и (2 ; 0).Но бывают случаи, когда точкой пересечения будет, например, точка (-3,14 ; 1), тогда графически вы не сможете определить точки пересечения, в таком случае используется аналитический метод.
Попробуем применить аналитический для вычисления точек пересечения. Для этого мы приравниваем уравнения y=4-x² и y=2-x
4-x²=2-x
x²-x+2-4=0
x²-x-2=0
применим теорему Виета для решения квадратного уравнения
x₁+x₂=1
x₁x₂= -2
x₁=2
x₂= -1

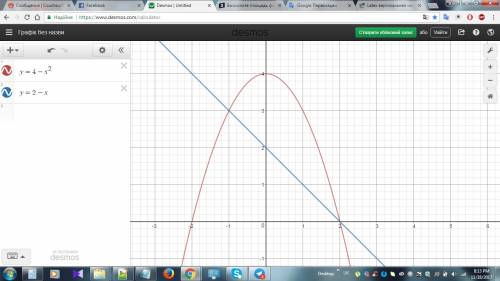
Теперь посмотрим где расположена фигура. Нам важно, какой график выше (относительно другого графика), а какой – ниже.

Из графика видно, что выше расположена парабола y=4-x² , а ниже прямая y=2-x.

Формула для вычисления площади: 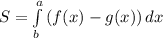$S= \int\limits^a_b {(f(x)-g(x))} \, dx$ где f(x) это функция которая расположена выше, чем функция g(x)

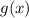
таким образом для исчисления площади нужно взять интеграл

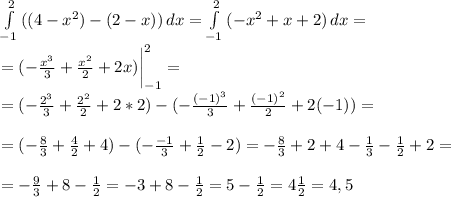
$\int\limits^2_{-1} {((4- x^{2} )-(2-x))} \, dx = \int\limits^2_{-1} {(-x^{2} +x+2)} \, dx = \\ = (-\frac{x^3}{3} +\frac{x^2}{2} +2x) \bigg|^2_{-1}= \\ =(-\frac{2^3}{3} +\frac{2^2}{2} +2*2) -(-\frac{(-1)^3}{3} +\frac{(-1)^2}{2} +2(-1)) = \\ \\ =(-\frac{8}{3} +\frac{4}{2}+4) -(-\frac{-1}{3} +\frac{1}{2} -2) = -\frac{8}{3} +2+4- \frac{1}{3} -\frac{1}{2} +2= \\ \\ = -\frac{9}{3} +8-\frac{1}{2} =-3+8- \frac{1}{2}=5- \frac{1}{2}=4 \frac{1}{2}=4,5$