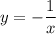и затем верхнюю часть графика отобразить в нижнюю(отрицательную часть)
(*)
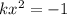и это уравнение решений не имеет при k>0(так как левая часть всегда положительно).
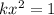и при k<0 это уравнение решений не имеет.
, имеем
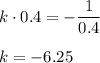
дано: треугольник KMN, AK=BN, AM=BM, CA перпендикулярно KM, CB перпендикулярно NM
доказать: MC - медиана треугольника KMN
В треугольнике KMN боковые стороны состоят из равных отрезков
AK=BN, AM=BM, следовательно
КМ=МК+АМ=ВN+MB=MN
Треугольник KMN - равнобедренный.
Δ КАС=Δ СВN,
так как это прямоугольные треугольники,
углы К и N равны как углы при основании равнобедренного треугольника,
катеты КА=ВN.
Если в прямоугольном треугольнике острый угол и катет равен острому углу и катету другого прямоугольного треугольника, то эти треугольники равны.
Следовательно, гипотенузы АС и CN этих треугольников равны.
АС=СN
Точка С - середина стороны КN
МС - медиана треугольника KMN, что и требовалось доказать.
4x^3+x^2-3x меньше или равно 2
выносим х за скобки, остается: х(4x^2+x-3)меньше или равно 2
получаем систему: x меньше или равно 2
4x^2+x-3 меньше или равно 2
4x^2+x-3-2 меньше или равно 0
приравниваем к нулю, получаем: 4x^2+x-3-2=0
4x^2+x-5=0
видим, что это квадратное уравнение
a=4, b=1, c=-5
D=81
x1=-10/8=-5/4
x2=1
рисунок решения в личку