Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.
Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.
1.
Пусть 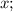
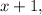

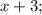
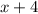 - пять последовательных натуральных чисел, тогда их сумма равна:
- пять последовательных натуральных чисел, тогда их сумма равна:
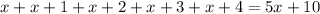
Очевидно, что каждое слагаемое 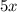 и
и 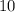 делится на 5, а это означает, что вся сумма делится на 5.
делится на 5, а это означает, что вся сумма делится на 5.
Доказано.
2.
Пусть 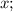
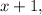

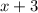 - четыре последовательных натуральных числа, тогда их сумма равна:
- четыре последовательных натуральных числа, тогда их сумма равна:
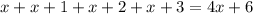
Очевидно, что первое слагаемое 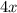 делится на 4, а второе слагаемое
делится на 4, а второе слагаемое 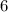 не делится на 4, это означает, что вся сумма не делится на 4.
не делится на 4, это означает, что вся сумма не делится на 4.
Доказано.
3.
Пусть 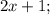
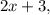
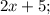
 - четыре последовательных нечётных натуральных числа, тогда их сумма равна:
- четыре последовательных нечётных натуральных числа, тогда их сумма равна:
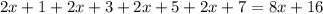
Очевидно, что каждое слагаемое 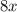 и
и 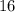 делится на 8, а это означает, что вся сумма делится на 8.
делится на 8, а это означает, что вся сумма делится на 8.
Доказано.
4.
Пусть 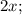
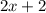 ;
; 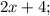
 - четыре последовательных чётных натуральных числа, тогда их сумма равна:
- четыре последовательных чётных натуральных числа, тогда их сумма равна:
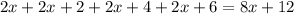
Очевидно, что каждое слагаемое 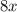 и
и 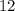 делится на 4, а это означает, что вся сумма делится на 4.
делится на 4, а это означает, что вся сумма делится на 4.
Доказано.