
Объяснение:
определяем производную
y'(x) = 12x³ + 12x² = 12x²(x+1)
y'(x) = 0 при
х1 = -1 - экстремум
х2 = 0 - экстремум
12x² всегда неотрицательно, как следствие:
y'(x) > 0 при х > -1
y'(x) < 0 при х < -1
у(х) убывает на х ∈ (-∞; -1)
у(х) возрастает на х ∈ (-1; 0) и (0; +∞)
х1 = -1 - экстремум - минимум
х2 = 0 - экстремум - перегиб
х ∈ (-∞; -1) - монотонно убывает
х ∈ (-1; 0) - монотонно возрастает
х ∈ (0; +∞) - монотонно возрастает
Точки для построения: в () - эксиремумы
х = {-2; (-1); -2/3; -1/2; -1/3; (0); 1/3; 2/3; 2}
y(-1) = 0;
y(0) = 1
остальные у - нужно посчитать
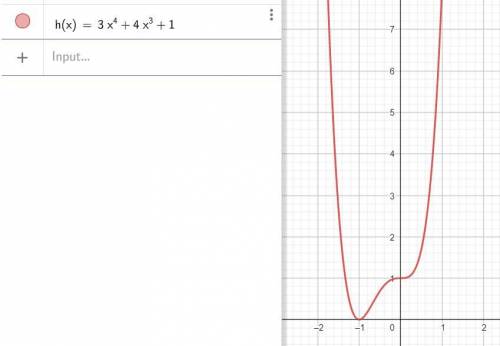
график - см. рис.
5x(2x +1) = 0 --> x = - 0.5
25 - 100x^2 = 25*(1 - 4x^2) = 25*(1 - 2x)(1+2x) --> x 1 = +0.5 x2 = - 0.5
25x^2 - 14 = 0; 25x^2 = 14 ; x^2 = 0.56 --> x = v 0.56
2x^2 - 8 = 0; 2x^2 = 8; x^2 = 4; x1= 2; x2 = -2
4x^2 - 12=0; 4x^2 = 12; x^2 = 3 ; x = v 3
x^2 - 10x = 0 ; x(x - 10) = 0--> x = 10
4x^2 + 20x = 0; 4x(x + 5)=0--> x = - 5
2x^2 + x = 0; x(x + 1) = 0 --> x = - 1
3x^2 - 27 = 0; 3(x^2 - 9)=0; 3(x-3)(x+3)=0--> x1 = 3; x2 = - 3
4x^2 + 20x = 0; 4x(x + 5) = 0; x = - 5