ответ: -0.1
Объяснение:
d = 5.12 - 5.30 = -0.18 (это убывающая АП)
an < 0
a1 + (n-1)*d < 0
5.3 + (n-1)*(-0.18) < 0
(n-1)*(-0.18) < -5.3
n-1 > 5.3/0.18
n-1 > 530/18
n-1 > 265/9
n-1 > 29.4... n€N
n-1 = 30
n = 31 --31 член АП будет первым отрицательным числом данной прогрессии (наибольшим из отрицательных), все следующие члены АП будут уже меньше...
а31 = 5.3 + 30*(-0.18) = 5.3 - 3*1.8 = 5.3 - 5.4 = -0.1
и можно проверить --вычислить предыдущий член АП (он будет еще положительным))
а30 = 5.3 + 29*(-0.18) = 5.3 - 5.22 = 0.08
Пусть число записано в виде произведения степеней простых множителей:
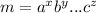, где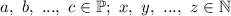 
Тогда, число делителей этого числа определяется по формуле:
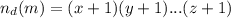
Рассмотрим некоторое число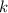 
. Пусть 
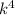имеет 85 делителей. Разложим число 85 на множители:
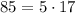
Заметим, что число 85 раскладывается на какие бы то ни было множители единственным образом.
Зная это, необходимо рассмотреть две ситуации.
1) Число делителей находилось как произведение из одного множителя (условное произведение):
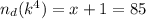
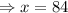
Тогда, число 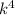имеет вид:
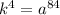
Найдем число :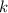
![k=\sqrt[4]{a^{84}}](/tpl/images/1399/3019/a4e5c.png)
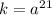
Найдем число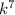 
:
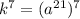
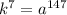
Число делителей этого числа:
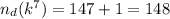
2) Число делителей находилось как произведение из двух множителей:
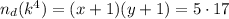
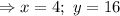
Тогда, число 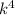имеет вид:
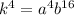
Найдем число :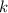
![k=\sqrt[4]{a^4b^{16}}](/tpl/images/1399/3019/39b3e.png)
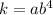
Найдем число :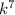
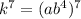
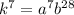
Число делителей этого числа:
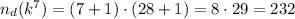
ответ: 148 или 232
(см. объяснение)
Объяснение:
Значит уравнение не имеет корней.
Уравнение решено!