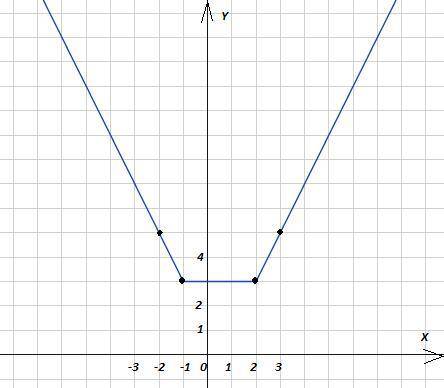
y = |x - 2| + |x + 1|
Нужно найти точки, в которых выражения под модулем меняют знак.
x - 2 = 0; x₁ = 2; x + 1 = 0; x₂ = -1
Эти точки разбивают числовую прямую на три интервала.
1) x ∈ (-∞; -1]
y = |x - 2| + |x + 1| = -x + 2 - x - 1 = -2x + 1;
y = -2x + 1 - линейная функция. Точки для построения
x₁ = -2; y₁ = 5; x₂ = -1; y₂ = 3
2) x ∈ (-1; 2)
y = |x - 2| + |x + 1| = -x + 2 + x + 1 = 3;
y = 3 - линейная функция. График - прямая, параллельная OX
3) x ∈ [ 2; +∞)
y = |x - 2| + |x + 1| = x - 2 + x + 1 = 2x - 1;
y = 2x - 1 - линейная функция. Точки для построения
x₁ = 2; y₁ = 3; x₂ = 3; y₂ = 5
Объяснение:
–5х – у + 4 = 0, -5х+4=у , коэффициент равен -5,значит функция убывает! Теперь раз функция проходит через начало координат,у нее нет свободного члена. У = - 5Х ,знак "-" означает убывание линейной функции..
проверка. (0,0) Следующую возьмем при х=1. у=-5*1=-5 -5∠0
(1,-5)