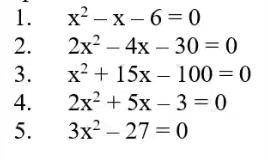
Чему равна вероятность того, что случайно выбранный горшок будет с дефектами (вероятность события A)?
Так как в данном случае вероятность - отношение числа благоприятных исходов к числу всех исходов, то:
P(A) = 28 / 400 = 0.07
Чему равна вероятность того, что случайно выбранный горшок не имеет дефектов (вероятность события B)?
Так как события A и B - противоположные, то есть ровно одно из них сбудется для одного произвольно выбранного горшка, то:
P(B) = 1 - P(A) = 1 - 0.07 = 0.93
Задача решена!
ответ: 0.93.
Объяснение:
1. x^2-x-6=0
D=(b^2)-4ac=1-4*(-6)=1-(-24)=25
x1=1+5/2= 3
x2=1-5/2= -2
2. 2x^2-4x-30=0
D= 16-4*2*(-30)=16-(-240)= 256
x1=4+4/4=2
x2=4-4/4=0
3. x^2+15x-100=0
D=225-4*(-100)=625
x1=-15+25/2= 5
x2= -15-25/2= -20
4. 2x^2+5x-3=0
D=25-4*2*(-3)=25-(-24)= 49
x1=-5+7/4= 0,5
x2= -5-7/4= -3
5. 3x^2-27=0
3x^2 = 27 ║:3
x^2 = 9
x = 3
x1 = 3
x2 = -3