(-5; 1; 1)
Объяснение:
Найдём уравнение прямой, перпендикулярной данной плоскости и проходящей через точку A. Направляющим вектором данной прямой является вектор нормали плоскости, то есть вектор {3; 2; 2}. Составим каноническое уравнение прямой:
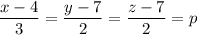
Из этого уравнения составим параметрическое уравнение:
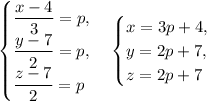
Чтобы найти точку пересечения прямой с плоскостью, то есть проекцию данной точки, подставим координаты из параметрического уравнения в уравнение плоскости:
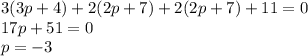
Подставляя найденное значение параметра, получим координаты искомой точки:
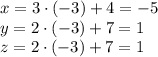
В решении.
Объяснение:
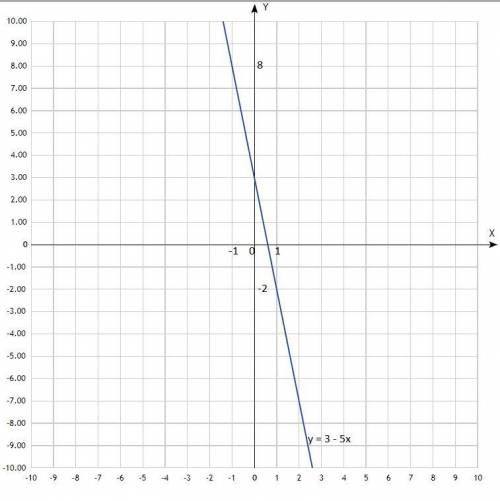
1) Постройте график функции у = 3 - 5х.
Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 3 - 5х
Таблица:
х -1 0 1
у 8 3 -2
По вычисленным точкам построить прямую.
2) Проходит ли график функции у = -5х + 4 через точку М(-7; 39)?
Нужно подставить известные значения х и у (координаты точки) в уравнение. Если левая часть равна правой, то проходит, и наоборот.
у = -5х + 4; М(-7; 39);
39 = -5*(-7) + 4
39 = 39, проходит.
3) Дана функция у = 1/4 х - 8. Найти значение функции, если значение аргумента равно 12.
Проще, найти значение у, если х = 12.
Подставить значение х в уравнение и вычислить у:
у = х/4 - 8
у = 12/4 - 8
у = 3 - 8
у = -5;
При х = 12 у = -5.
Объяснение:
1) Пересекаются т.к. уравнение 2x^2 = 7x + 9 имеет 2 корня. Находим их решая квадратное уравнение:
2x^2 - 7х - 9 = 0
D = 49 + 72 = 121 = 11^2
x1 = (7+11)/4 = 4.5; x2 = (7 - 11)/4 = -1
Подставим полученные значения x в функцию y = 2x^2 и получим координаты точек пересечения: (4.5, 40.5) и (-1, 2)
2) Парабола, ветви направлены вверх, координаты вершины: (0.5, -2.25), точки пересечения оси абсцисс:
(2, 0) и (-1, 0), точка пересечения оси ординат: (0, -2), функция положительна на промежутке (-∞, -1) U (2, +∞), функция отрицательна на промежутке (-1, 2), убывает на промежутке (-∞, 0.5), возрастает на промежутке (0.5, +∞), не является периодической, функция общего вида
3)
а) [15/16, +∞) б) [6.875, +∞)
4) не понял условие???