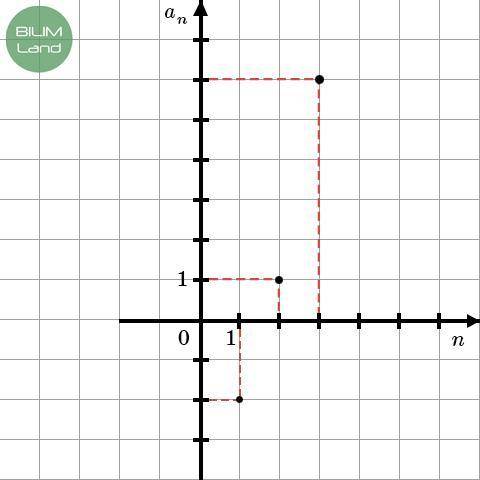
1) В таблицах значений.
2)Да, проходит.
Объяснение:
1) Построить график функции y = -3x + 6.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y = -3x + 6
Таблица:
х -1 0 1
у 9 6 3
2) Выяснить, проходит ли график функции через точку M(-20; 66)
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
M(-20; 66) y = -3x + 6
66= -3*(-20)+6
66= 60+6
66=66, проходит.
Найти частное решение линейного неоднородного уравнения 2-го порядка.
Алгоритм решения неоднородного ДУ следующий:
1) Сначала нужно найти общее решение соответствующего однородного уравнения y``+y`-2y=0
Составим и решим характеристическое уравнение:
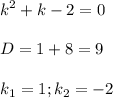
получены различные действительные корни, поэтому общее решение:
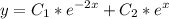
2) Теперь нужно найти какое-либо частное решение неоднородного уравнения
в правой части 4e²ˣ-2x+1. Значит предположу что частное решение неоднородного уравнения нужно искать в виде: y=Аe²ˣ+Bx+C
Найдём первую и вторую производную:
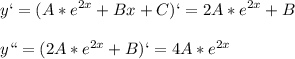
подставим в левую часть
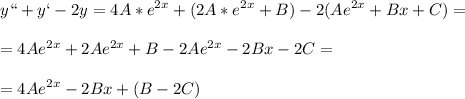
и теперь приравняем к правой
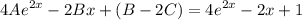
отсюда составим систему
![\displaystyle \left \{ {{4A=4; -2B=-2} \atop {B-2C=1}} \right. \]\\\\A=1; B=1;C=0](/tpl/images/3220/5151/2929a.png)
3) Запишем общее решение неоднородного уравнения:
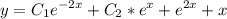
4) теперь найдем частное решение
y(0)=3; y`(0)=5
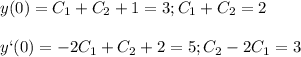
решая систему получим
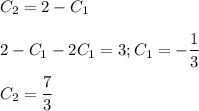
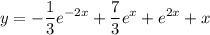
Объяснение:
141