Question

4sin(x)^2-1=0
решит
Заранее

Answer 1

ответ: sin(x)^2=1/4⇒sin(x1)=1/2⇒x1=π/6+2*π*N, x2=5*π/6+2*π*N

                                  sin(x3)=-1/2⇒x3=-π/6+2*π*N, x4=7*π/6+2*π*N.

Объяснение:

Answer 2

Объяснение:

4sin²x-1=0

4sin²x+0sinx-1=0

Замена: Sinx=t

4t²-1=0

D=b²-4ac=0²-4×4×(-1)=16

$t1,2= \frac{-b \pm \sqrt{D} }{2a} = \frac{-0\pm \sqrt{16} }{2 \times 4} = \frac{\pm \sqrt{16} }{8} = \pm \frac{\pm 4}{8}$

$t1 = \frac{4}{8} = \frac{1}{2}$

$t2 = - \frac{4}{8} = - \frac{1}{2}$

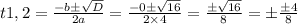
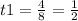
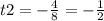
Обратная замена:

t=sinx

sinx1=1/2

arcsin1/2=x

x=π/6+2πn, nєZ

х=5π/6+2πn, nєZ

sinx2=-1/2

arcsin(-1/2)=x2

x2=-arcsin1/2

x=-π/6+2πn, nєZ

x=7π/6+2πn, nєZ

х=π/6+2πn, nєZ

х=5π/6+2πn, nєZ

x=-π/6+2πn, nєZ

x=7π/6+2πn, nєZ