Объяснение:
Проверим случай p=5, уйдет квадратичная часть, но линейная останется, значит неравенство не будет выполняться для всех x.
При p не равном 5 график левой части неравенства представляет собой параболу, для того, чтобы неравенство было верно для любого x вся парабола должна лежать ниже оси абсцисс, т. е. ветви вниз(p-5<0) и D(дискриминант)<0.
D1=(2p-4)^2-4(p-5)(-p-3)=8p^2-24p-44<0
2p^2-6p-11<0
D2=36+88=124
p1=(3-sqrt(31))/2
p2=(3+sqrt(31))/2
D1<0 при
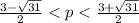
Эти значения p меньше пяти(т.е. ветви направлены вниз). Заносим их в ответ.
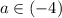
1) ООО
2) ООР
3) ОРО
4) ОРР
5) РОО
6) РОР
7) РРО
8) РРР
Вероятность находится по формуле P=A/Aв, где A - количество подходящих под условие случаев, Ав - количество всех случаев. Соответственно во всех задачах ниже Ав=8.
а) Количество случаев, где в последний раз выпадает решка - 4.
P=4/8=1/2=50%.
б) Такой случай только 1. P=1/8=12.5%.
в) Таких случаев 3. P=3/8=37.5%.
г) Таких случаев 4. P=4/8=1/2=50%.