х+2- скорость катера по течению
х-2- скорость катера против течения
40/(х+2)+6/(х-2)=3
40х-80+6х+12=3(х+2)(х-2)
46х-68=3(х^2-4)
46х-68=3х^2-12
3х^2-46х+56=0
D=46^2-4•3•56=1444
x=(46+38)/6=14 км/ч- скорость катера
1) Если требуется найти ВСЕ ОБЩИЕ РЕШЕНИЯ нескольких уравнений, то говорят, что надо решить систему уравнений.
2) Решением системы уравнений с двумя переменными называют ПАРУ ЗНАЧЕНИЙ ПЕРЕМЕННЫХ,ОБРАЩАЮЩУЮ КАЖДОЕ УРАВНЕНИЕ В ВЕРНОЕ РАВЕНСТВО.
3) Решить систему уравнений - это значит НАЙТИ ВСЕ РЕШЕНИЯ ИЛИ ДОКАЗАТЬ,ЧТО РЕШЕНИЙ НЕТ.
4) Суть графического метода решения системы уравнений состоит в следующем:
а) построить на одной координатор плоскости ГРАФИКИ УРАВНЕНИЯ, ВХОДЯЩИЕ В СИСТЕМУ.
б) найти КООРДИНАТЫ ВСЕХ ТОЧЕК ПЕРЕСЕЧЕНИЯ ПОСТРОЕННЫХ ГРАФИКОВ
в) ПОЛУЧЕННЫЕ ПАРЫ ЧИСЕЛ и будут искомыми решениями
5) Если одно из уравнений системы не имеет решений, то вся система РЕШЕНИЙ НЕ ИМЕЕТ.
6) Если каждое уравнение системы линейных уравнений имеет решение и графиком одного из уравнений является вся плоскость, то система имеет БЕСКОНЕЧНО МНОГО РЕШЕНИЙ.
7) Если графиками уравнений, входящих в систему линейных уравнений, являются прямые, то количество решений этой системы зависит от ВЗАИМНОГО РАСПОЛОЖЕНИЯ ДВУХ ПРЯМЫХ НА ПЛОСКОСТИ:
а) если прямые ПЕРЕСЕКАЮТСЯ, то система имеет единственное решение
б) если прямые СОВПАДАЮТ, то система имеет бесконечно много решений
в) если прямые ПАРАЛЛЕЛЬНЫ, то система решений не имеет.
Объяснение:
В решении.
Объяснение:
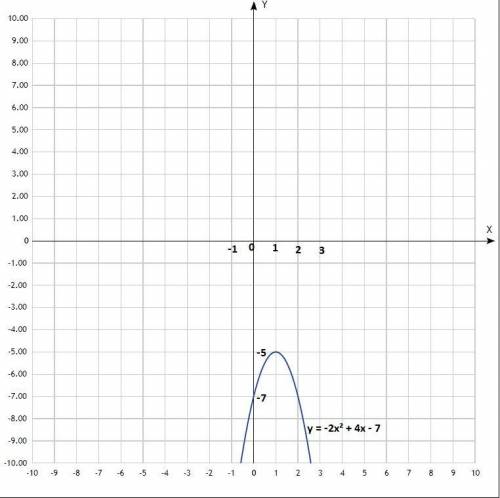
1. Дана функция у = -2х² + 4х - 7;
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вниз (коэффициент при х²<0);
Построить график.
1) Найти координаты вершины параболы:
у = -2х² + 4х - 7;
а) Найти х₀ по формуле:
х₀ = -b/2a;
х₀ = -4/-4
х₀ = 1;
б) Найти у₀:
у = -2х² + 4х - 7;
у₀ = -2 * 1² + 4 * 1 - 7 = -2 + 4 - 7 = -5
у₀ = -5;
Координаты вершины параболы: (1; -5).
2) Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = -2х² + 4х - 7;
Таблица:
х -1 0 1 2 3
у -13 -7 -5 -7 -13
По вычисленным точкам построить параболу.
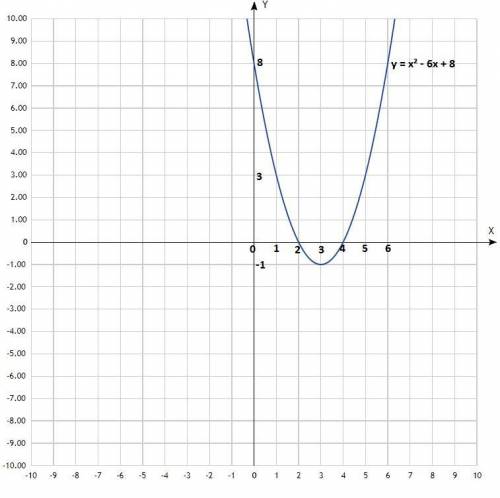
2. Дана функция у = х² - 6х + 8;
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вверх (коэффициент при х²>0);
Построить график.
1) Найти координаты вершины параболы:
у = х² - 6х + 8;
а) Найти х₀ по формуле:
х₀ = -b/2a;
х₀ = 6/2
х₀ = 3;
б) Найти у₀:
у = х² - 6х + 8;
у₀ = 3² - 6 * 3 + 8 = 9 - 18 + 8 = -1
у₀ = -1;
Координаты вершины параболы: (3; -1).
2) Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 6х + 8;
Таблица:
х 0 1 2 3 4 5 6
у 8 3 0 -1 0 3 8
По вычисленным точкам построить параболу.
х км\ч скорость катера
(х-2) км\ч скорость катера против течения
(х+2) км\ч скорость по течению
40/(х+2) - время, затраченное на путь по течению
6/(х-2) - время, затраченное на путь против течения
40/(х+2) +6/(х-2)=3 умножим на (х-2)*(х+2)
40(х-2)+6(х+2)=3(х^2-4)
40x-80+6x+12-3x^2+12=0
-3x^2+46x-56=0
3x^2-46x+56=0
D=46^2-4*3*56=2116-672=1444
x=(46±38)/6
x1=14 км/ч
x2=8/6=1⅓ - не удовл.