Число делится на 10 только в том случае, если оно оканчивается цифрой 0.
Посмотрим, какой цифрой оканчивается каждое слагаемое.
1) число 7 в разных степенях оканчивается разными цифрами. Попробуем установить закономерность.
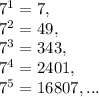
Т.е. последние цифры записи степеней семерки чередуются так: 7 - 9 - 3 - 1 и по кругу.
Т.к.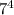 
оканчивается цифрой 1, то 
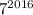также оканчивается цифрой 1. Тогда число 
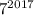оканчивается цифрой 7.
2) Для степеней четверки закономерность проще - 4 - 6 и по кругу:
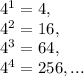
Поскольку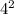 
оканчивается цифрой 6, то 
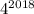также оканчивается цифрой 6.
3) Закономерность для степеней тройки - 3 - 9 - 7 - 1 и по кругу:
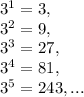
Т.к.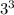 
оканчивается цифрой 7, то 
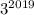также оканчивается цифрой 7.
В итоге слагаемые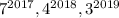 
оканчиваются цифрами 7, 6 и 7 соответственно. Если их сложить, то в разрядке единиц класса единиц получим 0. Т.е. число 
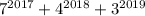оканчивается цифрой 0 - следовательно, оно таки делится на 10.
ОТВЕТ: да.
Если Вы помните, рациональные числа были введены потому, что во множестве целых чисел не всегда можно выполнить деление. Например, существует целое число, которое является результатом деления 8 на 2, но не существует целого числа, которое является результатом деления 8 на 3. Поэтому были введены рациональные числа, то есть дроби вида p/q. Целые числа стали их подмножеством, когда q=1.
Для выполнимости деления рациональных чисел достаточно, но вот для извлечения корней - нет. Например, не существует рационального числа, которое было бы результатом извлечения квадратного корня из двух. (Это доказывается в Вашем учебнике, я уверен. Если не поняли, напишите, объясню.) Поэтому производят дальнейшее расширение системы чисел. К рациональным числам добавляют ещё и иррациональные, и все они вместе образуют множество действительных чисел.
Если не вдаваться в подробности, то рациональные числа можно отличить от иррациональных следующим образом. Рациональные числа, если их записать десятичной дробью, обязательно дадут конечную или бесконечную периодическую дробь. Это тоже легко доказать. Иррациональные же числа, записанные в виде десятичной дроби, оказываются представленными бесконечной НЕпериодической дробью.
Типичным примером иррационального числа является корень квадратный из двух. Пи - тоже иррациональное число, причем в определенном смысле более сложное, чем корень из двух, потому что Пи нельзя представить в виде корня из рационального числа. Но это уже немножко высший пилотаж