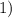
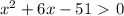
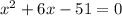
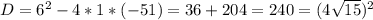
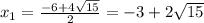
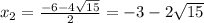
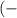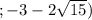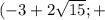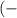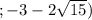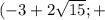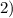
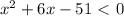
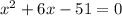
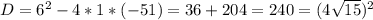
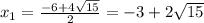
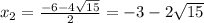
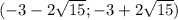
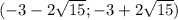
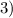
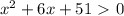
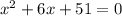
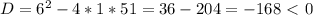
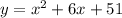
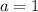∈ 
∞ 
∪ 
∞ 
∞ ∪ ∞ 
∈ 
положительный, то ветви параболы направлены вверх, а поскольку 
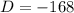отрицательный, то парабола не пересекается с осью 
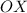. Поэтому парабола 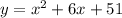расположена над осью 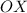; таким образом, при любом значении x имеем y>0. Значит, 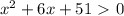при любом значении x. ∞ 
∞ 
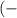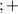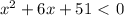
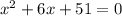
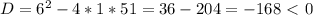
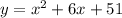
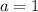положительный, то ветви параболы направлены вверх, а поскольку 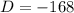отрицательный, то парабола не пересекается с осью 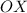. Поэтому парабола 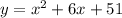расположена над осью 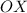; таким образом, при любом значении x имеем y>0. Значит, 
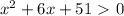при любом значении x. Следовательно, рассматриваемое неравенство не имеет решений. 
Пусть функция f(x) непрерывна и определена на заданном отрезке [a; b] и имеет на нем некоторое (конечное) количество критических точек. Первым делом найдем производную функции f'(x) по х.
2Приравниваем производную функции к нулю, чтобы определить критические точки функции. Не забываем определить точки, в которых производная не существует - они также являются критическими.
3Из множества найденных критических точек выбираем те, которые принадлежат отрезку [a; b]. Вычисляем значения функции f(x) в этих точках и на концах отрезка.
4Из множества найденных значений функции выбираем максимальное и минимальное значения. Это и есть искомые наибольшее и наименьшее значения функции на отрезке.