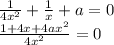
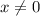и перейдем к следующему уравнению: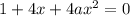
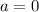, то получим линейное уравнение: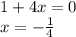
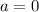удовлетворяет заданному условию.
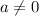, то получаем квадратное уравнение, наличие решений у которого зависит от дискриминанта: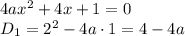
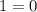, значит остается единственный вариант: приравнять дискриминант к нулю и проверить, будет ли уравнение в этом случае иметь единственный корень: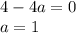
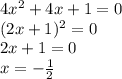
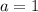также удовлетворяет заданному условию.
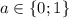, тогда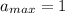 
y = - 33
Берем производную, она равна 2 - 242/x^2, приравуниваем ее к нулю и находим х:
x1 = - 11, x2 = 11.
В данный нам отрезок попадает лишь х = 11.
Считаем значение функции в каждой из этих точек:
- 16 (нижняя граница отрезка) y = - 36,125
- 11 (найденная нами точка) y = - 33
- 0,5 (верхняя граница отрезка) y = - 111
И затем выбираем наибольшее из полученных значений.