Тільки по графіку можна одразу вказати, при яких значеннях аргументу значення функції додатні
Приклад: Використовуючи графік функції у = х2 – 1, де -3 ≤ х ≤ 2, знайти значення аргументу, при яких функція набуває додатних значень;
Для значень х таких, що -3 < х < -1, точки графіка розташовані вище осі абсцис. Тому функція набуває додатних значень при -3 < х < -1. Так само вище осі абсцис знаходяться точки графіка для 1 < х < 2. Тому при 1 < х < 2 функція знову набуває додатних значень. Отже, при -3 < х < -1 або 1 < х < 2 функція набуває додатних значень.
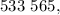 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).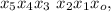


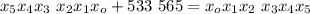 ;
;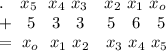

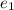 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого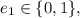
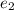 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго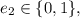
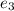 – возможная добавочная единица,
– возможная добавочная единица,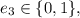
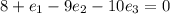 ;
;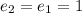 и при
и при  ;
;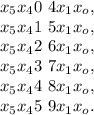
 поскольку
поскольку 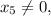 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.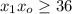 .
.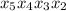 .
.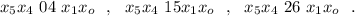
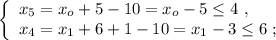

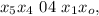
 может играть роль апреля.
может играть роль апреля.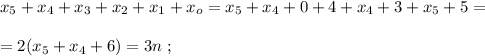
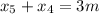 ;
;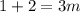 ;
;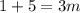 ;
;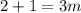 ;
; ;
;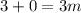 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.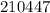 – дата 21/04/47 г.
– дата 21/04/47 г.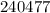 – дата 24/04/77 г.
– дата 24/04/77 г.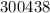 – дата 24/04/38 г.
– дата 24/04/38 г.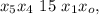
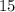 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;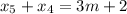 ;
;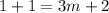 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

Пусть х км/ч скорость катера, тогда скорость водного мотцикла х+6 км/ч. Время катера в пути 36/х часов, время водного мотоцикла 36/(х+6) часов. Время катера на 1/2 часа больше, чем время водного мотоцикла. Составим и решим уравнение:
36/х - 1/2 = 36/(х+6)
Все переносим в левую часть и приводим к общему знаменателю, получаем вот что:
(-x²-6x+432)/(2x(x+6)) ОДЗ: х≠0, -6
решаем квадратное уравнение, умножив его на мину один:
х²+6х-432=0
D= 36+ 1728=1764=42²
корни этого уравнения: 18 и -24 (-24 не подходит по смыслу задачи)
Значит 18 км/ч, скорость катера, тогда скорость водного мотоцикла 18+6=24 км/ч
ответ: 18 км/ч и 24 км/ч