Здесь бы уточнить какой алфавит у кодового замка, это набор из цифр от 1 до 9 или от 0 до 9. Разберу для обоих случаев.
Для первого случая получается следующее, если мы хотим, чтобы в коде замка попадались хотя бы 2 одинаковые цифры, то это значит, что на любые две позиции замка должно приходиться одинаковое количество доступных на выбор цифр, т. е. пусть две подряд идущие позиции кодового замка будут иметь одинаковые цифры, тогда на каждую из них приходится по девять цифр, а на остальные две по восемь и семь цифр соответственно. Перемножаем эти количества и получаем ответ
9•9•8•7=4536.
Для алфавита, состоящего из 10 цифр, ход рассуждения тот же, поэтому имеем
10•10•9•8=7200.
(Если я не ошибся то получаеться так)
Сколько четырехзначных чисел можно составить из цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9?
Александр Сергеевич Македонский
Сингулярист, любитель занимательной математики, распространитель идей
а чего такие сложные решения? комбинаторика. факториал? Отвечаю для школьника 3 класса: Всё ведь просто: 1000, 1001, 1002, , 9998, 9999. Итого: 10000-1000=9000
Ровно девять тысяч чисел. Без повторов, да, нужен комбинаторный анализ
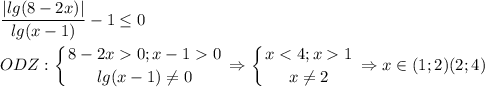
1) раскроем модуль при lg(8-2x)≥0
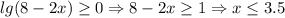
тогда
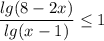
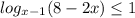
далее применим метод рационализации
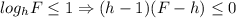
получаем
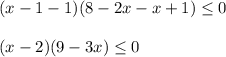
и метод интервалов
x=2; x=3
___-_____2__+____3___-___
1 по условию 3,5
тогда в первом случае x∈ (1;2)∪ [3;3.5]
2) раскроем модуль lg(8-2x)<0
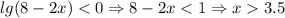
тогда
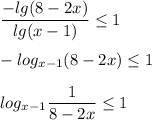
метод рационализации
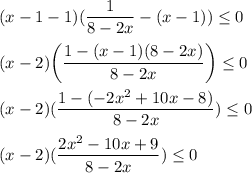
x=2; x≠4; x= 2.5 ±0,5√7 (это х ≈ 3,82 и х≈1,17)
_-___2,5-√7___+___2_____-______2,5+0,5√7__+____4___-___
3,5 по условию 4
тогда во втором случае х∈(3,5; 2.5+0.5√7]
3) и теперь все объединяем
х∈ (1;2)∪ [3; 2.5+0.5√7]
Объяснение: