всё это сводится к простому показательному ур-ию
2^(4-x)=17-2^(x)
2^(x)=t, t>0
16/t-17+t=0
t^2-17t+16=0
D=225>0
t=1
t=16
обратная замена и 2 случая:
1) 2^(x)=1 при х=0
2) 2^(x)=16 при х=4
ОТВЕТ: 0; 4
 , где A, B, C - координаты нормального вектора плоскости N(A,B,C).
, где A, B, C - координаты нормального вектора плоскости N(A,B,C). ⇒ N(2,-3,4).
⇒ N(2,-3,4). , где
, где 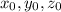 - координаты точки M(
- координаты точки M(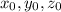 ), через которую проходит прямая,
), через которую проходит прямая,  - координаты направляющего вектора S(
- координаты направляющего вектора S( ).
). ) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).
) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).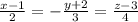
О каком дискриминанте речь?
Вначале хотелось бы узнать основание логарифма, стоящего в правой части уравнения.
Подозреваю, что это 2.
Тогда все получается.
будьте внимательны!